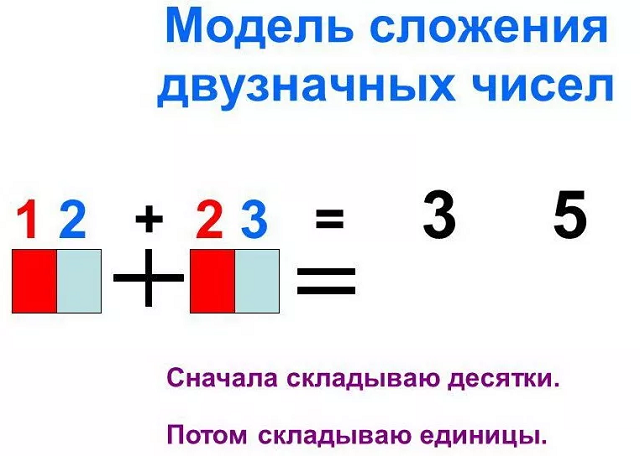
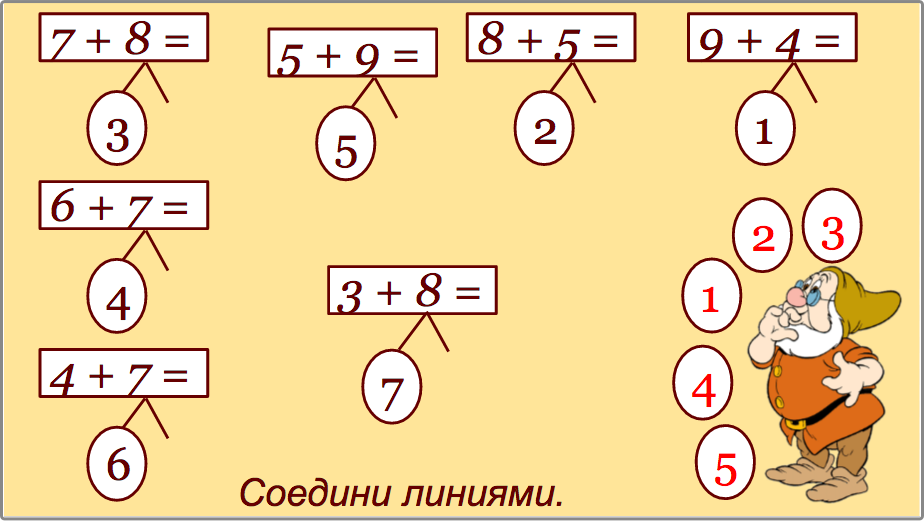
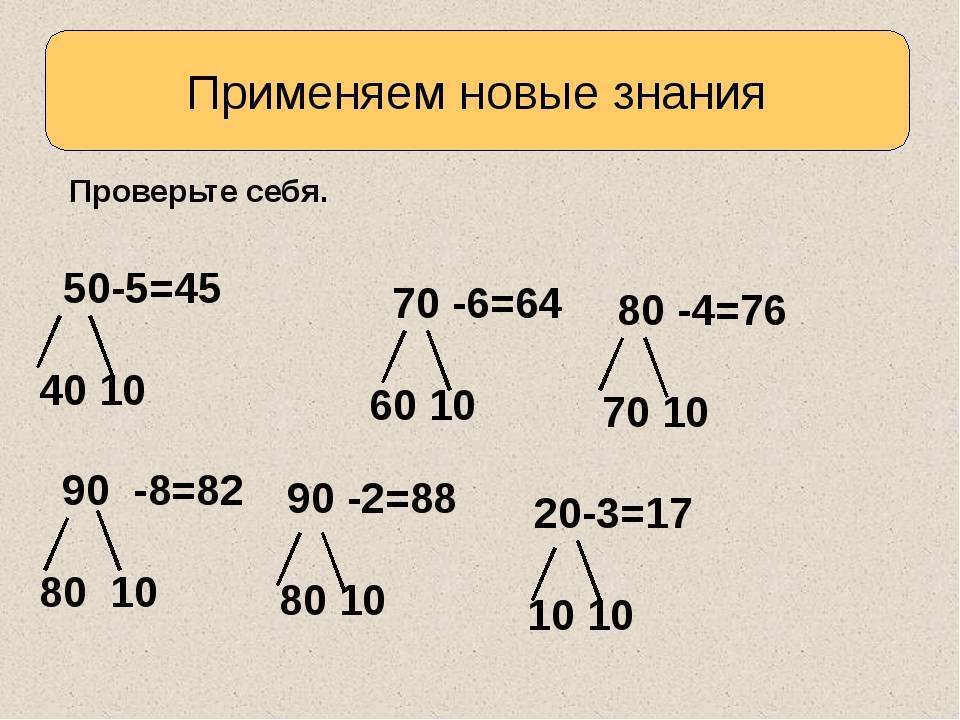
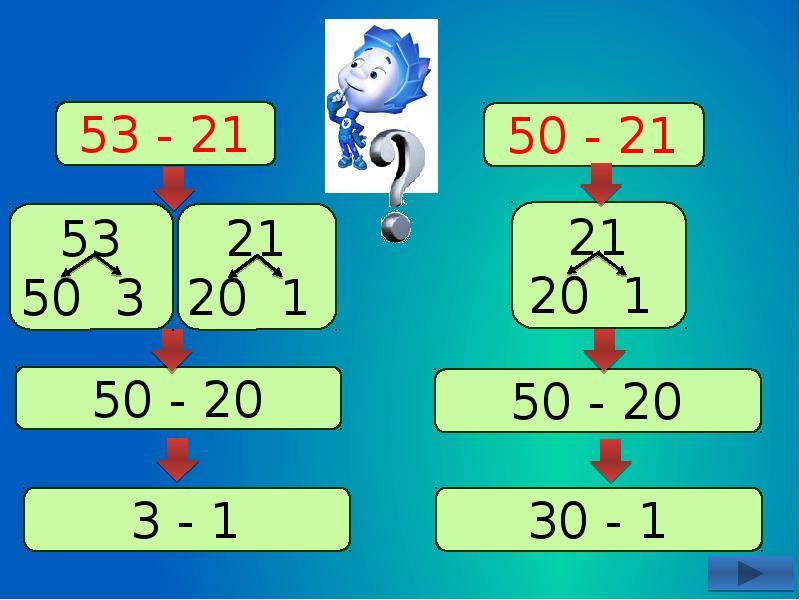
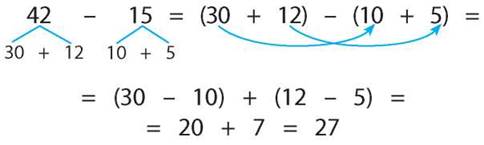Секреты устного счёта
Существуют приемы устного счета – простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем – единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел – это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения – это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения – с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
умножить на 4 – это дважды умножить на 2;
умножить на 6 – это значит умножить на 2, а потом на 3;
умножить на 8 – это трижды умножить на 2;
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
разделить на 4 – это дважды разделить на 2;
разделить на 6 – это сначала разделить на 2, а потом на 3;
разделить на 8 – это трижды разделить на 2;
разделить на 9 – это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 – это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 – 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко – это примеры занимательные, так называемые маленькие хитрости.
Высчитывание процентов
Многие люди впадают в ступор, когда их просят найди 6 процентов от 253. Однако если знать основные математические правила, то в этом нет абсолютно ничего сложного. Причем, чтобы научиться проводить все действия в уме, не потребуется нескольких лет практики. Достаточно лишь следовать определенному алгоритму действий:
- Найти 1% от имеющегося числа. Для этого его необходимо разделить на 100: «253:100=2,53».
- Разложить получившиеся число на слагаемые, которые будет легко умножить на 6: 2,53=2+0,5+0,03.
- Провести умножение: 2*6=12, 0,5*6=½*6=3, 0,03*6=0,18.
- Сложить получившиеся значения: 12+3+0,18=15+0,18=15,18.
Чтобы научиться считать числа в уме, вовсе не обязательно быть вундеркиндом или потратить годы практики. Достаточно просто знать основные правила и формулы, которые позволяют упростить те или иные действия, а также уметь грамотно заменить некоторые переменные. Ну и, пожалуй, важнее всего — концентрироваться на выполнении определенной задачи. Если решать такие примеры каждый день, то со временем от калькулятора можно будет отказаться вовсе, что очень удобно, ведь даже в век информационных технологий полностью положиться на машины нельзя.
Проверка результата вычитания сложением
Проверка результата вычитания двух натуральных чисел базируется на связи между вычитанием и сложением. Там мы выяснили, что если c+b=a, то a−b=c и a−c=b. Если a−b=c, то c+b=a; если a−c=b, то b+c=a. Докажем справедливость данных равенств.
Пусть из a отложили в сторону b, после чего осталось c. Этому действию соответствует равенство a−b=c. Мы вернем отложенные b на место, то плучим a. Тогда можно говорить о справедливости равенства c+b=a.
Теперь мы можем сформулировать правило, позволяющее проверить результат вычитания сложением: нужно к полученной разности прибавить вычитаемое, при этом должно получиться число, равное уменьшаемому. Если полученное число не равно уменьшаемому, то при вычитании допущена ошибка.
Осталось лишь разобрать решения нескольких примеров, в которых выполняется проверка результата вычитания при помощи сложения.
Пример 24
Из 50 было вычтено 42 и было получено 6. Правильно ли было выполнено вычитание?
Проверим полученный результат вычитания. Для этого прибавим к полученной разности вычитаемое: 6+42=48 (если нужно, изучите другие параграфы по данной теме). Так как мы получили число, не равное уменьшаемому 50, то можно утверждать, что вычитание было проведено неправильно. Была допущена ошибка.
Пример 25
Необходимо определить разность 1 024−11 и проверить результат.
Вычисляем разность: 1 024−11=1 024−(1+10)=(1 024−1)−10=1 023−10=1 013.
Теперь выполняем проверку:
1 013+11=(1 000+10+3)+(10+1)==1 000+10+10+3+1=1 000+20+4=1 024
Получили число, равное уменьшаемому, следовательно, разность вычислена правильно. 1 024−11=1 023.
Работа с бумагой
 Все дети очень любят рисовать, к тому же все они любят положительную реакцию родителей на это. После того, как удалось обучить ребёнка теоретическому подсчёту, нужно переходить к практической работе. Чтобы было проще объяснить ребёнку, почему каждая цифра пишется именно так, то следует запомнить одно простое правило – у каждой цифры своё количество углов. Т.е. у единицы всего 1 угол, тогда как у восьмёрки их 8.
Все дети очень любят рисовать, к тому же все они любят положительную реакцию родителей на это. После того, как удалось обучить ребёнка теоретическому подсчёту, нужно переходить к практической работе. Чтобы было проще объяснить ребёнку, почему каждая цифра пишется именно так, то следует запомнить одно простое правило – у каждой цифры своё количество углов. Т.е. у единицы всего 1 угол, тогда как у восьмёрки их 8.
Подобный наглядный пример достаточно легко сможет сориентировать дитя, но в процессе нужно быть готовым к «изобретению» новых чисел, которые ни в коем случае нельзя забраковывать. Пусть будут – потом сами отпадут.
Для начала желательно приобрести любые детские обучающие тетради, которых с каждым годом становится всё больше. Основное их удобство – это наличие уже готовых рисунков, благодаря чему ребёнок будет видеть, что именно он складывает или вычитает. Результаты можно доверить записывать самостоятельно, хотя и первые попытки будут весьма неуклюжими. Со временем в этих же тетрадях яблоки и шишки будут заменяться на цифры, что станет новым шагом в развитии.

- Прописи «Учимся писать цифры. Рабочая тетрадь для детей 5-6 лет» от Елены Бортниковой
- Прописи Л. Мавриной «Дружок. Прописи для дошкольников. Учимся писать цифры»
- И оригинальные многоразовые карточки «Я учусь писать цифры» от Бурже, Бруст, Курвуазье
Виды
На уроках на устный счет отводится мизерное время, но это не умаляет его значения для развития мыслительной деятельности ребят. Навыки устных вычислений формируются на уроках математики в начальной школе при выполнении разнообразных видов заданий и упражнений.

Сравнить математические выражения
Подобные задания отличаются вариативностью:
- определить равенство либо неравенство двух данных выражений (предварительно найдя и сравнив их значения);
- к заданным знаку отношению и одному из выражений составить второе выражение или дополнить незаконченное предложенное;
- в таких упражнениях в выражениях могут использоваться однозначные, двузначные, трехзначные числа и величины и все четыре арифметических действия. Главное назначение подобных заданий – прочное усвоение теоретического материала и отработка вычислительных навыков.

- Решить уравнения. Они помогают усвоить связи между компонентами и результатами арифметических действий.
- Решить задачу. Это могут быть и простые и составные задачи. С их помощью укрепляются теоретические знания, вырабатываются вычислительные умения и навыки, активизируется мыслительная деятельность детей.

Обучающие материалы для счета
Научить в возрасте от 3-5 лет достаточно сложно. Для обучения на начальной стадии можно применять разные наглядные материалы
, в частности:
- картинки;
- цифры на магните;
- кубики и прочее.
Когда обучение переходит к сложению и вычитанию
, то в качестве наглядных материалов применяют:
- пальцы – предлагайте детишкам сосчитать количество пальцев на руке, затем загибайте и спрашивайте, сколько их осталось;
- палочки – по аналогии с пальчиками;
- линейку – покажите цифры на линейке и деления, отсчитывайте их, если хотите научить малыша сложению.
Однако многие психологи не поощряют применение таких приспособлений для того, чтобы научить малышей считать, и полагают, что это провоцирует лень, а мышление и память не тренируется. Ряд специалистов предлагает учить детей счету исключительно устно.
Как пользоваться пальцами без использования счетов
Конечный результат обучения ментальному счету – это решение арифметических задач на пальцах, без абакуса. Знакомство с этим методом практической работы начинайте с простых упражнений.
Считать на пальцах нужно следующим образом:
- Представьте, что рука — это абакус.
- Пальцы левой руки отвечают за числа, кратные 10. Большой палец – это 50.
- Правая рука — это числа от 1 до 9, большой палец обозначает цифру 5.
- Сжатые кулаки — 0.
Приведем несколько примеров счета на руках.
Показываем число 98
Разворачиваем все пальцы левой руки. Они обозначают цифру 90. На правой руке поднят большой палец – это 5, и три других пальчика. В итоге получается 90 и 8.
С помощью счета без абакуса можно складывать, отнимать, делить и умножать.
Пальчики выполняют роль костяшек. Спустя 10–12 уроков по ментальной карте, то есть с помощью визуализации, ребенок будет решать примеры довольно быстро.
Именно этот метод является эффективным способом обучения быстрому счету. Ребенок не будет тратить время на передвижение бусин на счетах, запоминать их расположение. Движения пальцами автоматизируются поэтапно, от простых примеров к сложным.
Математика для дошкольника: что ещё пригодится в 1 классе?
Ориентация в пространстве
“Где левая рука? Закрой правый глаз. Возьмись за левое ухо. Попрыгай на левой ноге. Сколько справа от тебя машин? А слева? А спереди (перед)? А позади (за)? Каким цветом машина стоит между серой и зелёной? Что находится под столом? На столе? Над столом? Около? Рядом? Внутри (в)? Снаружи (с/со)? Кто встал из-за стола? Что я достала из-под стола?”
Мы играли в такие игры.
Ведущий (то я, то сын) на улице давал указания закрывшему глаза: “Помедленней, впереди кочка, осталось два шага, раз, два, теперь высоко поднимай правую ногу… Сзади на тебя идёт мужчина, подвинься влево, ещё немного… Навстречу едет велосипедист, быстрей два шага вправо.”
Ведущий (то я, то сын) рисовал план комнаты, на нём крестиком отмечал где спрятана игрушка, которую с помощью плана нужно было найти второму игроку.
Я раскладывала записочки по квартире с указанием где находится следующий листочек: “В столе на кухне”, “Под диваном”, “Над твоей кроватью”… В последней записке говорилось, где лежит клад. Первая отдавалась сыну.
я давала (плюс что-то делали в клубе), чтобы убедиться, что проблем с ним нет: “От точки две клетки вверх, одну по диагонали, при вправо…”
И проверяла на листке бумаги: “В верхнем правом углу нарисуй звезду. В центре цветочек. Слева от цветочка круг. По середине нижнего края листка поставь крестик…”
Подготовка к умножению
В шесть лет полезно изучить как сгруппированы минуты на часах (по 5), почему показывая на «2» мы говорим о 10 минутах.
Интересны задачи и на объединения по два: “Из под забора видны шесть лапок. Сколько цыплят прячется за забором?” или “Сколько варежек нужно 4-м ребятишкам?”.
следующий пример
По три цветка может стоять в 4 вазах, по шесть рыбок плавать в 3 аквариумах и т.п.
Базовые шаги
Здесь потребуются различные предметы, которые только смогут заинтересовать ребёнка – кубики, палочки, шишки, яблоки, камешки, куклы и абсолютно все, что поддаётся счёту.
Знаки «+», «-» и «=» придётся изготовить из палочек либо доверить этот процесс ребёнку.
Начинать лучше с самого простого, т.е. как объяснить ребёнку сложение. Но в этот процесс в любом случае придётся включать и вычитание, поэтому удастся «убить сразу 2-х зайцев»:
Данный шаг самый ответственный, поэтому ребёнок должен получать максимальное удовольствие от игры. Запоминание должно происходить бессознательно, но в исключительных случаях ребёнок сам заинтересовывается процессом, благодаря чему дальнейшая работа упрощается в разы. Если попробовать заставлять, то этим можно лишь вызвать антипатию к дальнейшему обучению.
Техники знакомства с цифрами
Существует огромное количество разнообразных методик, благодаря которым можно обучить ребенка цифрам. Выбрать правильную — непросто, поскольку часто приверженцы одной техники яро критикуют другие и наоборот.
Мы приведем самые распространенные варианты:
подручные материалы. Это могут быть кубики, фломастеры, вагоны поезда, мягкие игрушки и прочее
Важно, чтобы ребенок мог соотнести конкретную цифру и число предметов. То есть, если на листе написано «3», рядом должно лежать 3 кубика, а еще лучше — построить из них башенку
Также можно взять небольшую коробочку, складывать в нее однотипные предметы и просить ребенка сказать, сколько их лежит внутри;
цифры — на видных местах. Можно развесить магниты на холодильник или просто карточки в разных частях дома. Главное, чтобы рядом с цифрой было изображено количество предметов ей соответствующее;
обучающие мультфильмы. В сети можно найти десятки видеоматериалов, в которых игрушечные герои учат мальчишек и девчонок, как выглядят цифры. Такие мультфильмы можно использовать иногда, например, для закрепления пройденного материала;
пальцы рук. Легко научить ребенка цифрам, соотнося их с количеством пальцев. Однако, некоторые специалисты считают этот метод не слишком удачным, поскольку позже ребенок будет использовать его при обучении счету. А это мешает развитию мыслительных навыков (пальцы всегда рядом, думать не нужно, достаточно посчитать их);
разучивание небольших дву- или четверостиший с названиями цифр — это улучшает запоминание (включается не только зрительная, но и слуховая память).
Специалисты рекомендуют не ограничивать фантазию детей — если малыш любит игры с пластилином или тестом, циферки можно и нужно лепить, если обожает возиться с красками, наглядные пособия можно рисовать вместе с мамой и т.д.
Вот и польза от интернета
Чтобы научить ребенка считать в уме, можно скачать ему на телефон специальное приложение, в котором есть огромное количество различных примеров, на решение которых дается от 2 до 5 секунд. Само собой, можно попытаться составить уравнения и задачи самому, однако практика показывает, что в большинстве случаев они получаются крайне однообразными и не несут большой пользы. Также существуют специальные сайты, которые позволяют своим посетителям решать уравнение и сложные задачки в режиме онлайн. Используя такие платформы, самое главное — подобрать под себя правильный уровень сложности.
Чтобы система обучения приносила как можно большую пользу, важно понять, что вовсе не обязательно часами сидеть за примерами или пытаться решить сложные задачи сразу в уме. Ментальный счет — это долгий и кропотливый процесс, который не терпит спешки, и чтобы учиться правильно, достаточно уделять примерам от 5 до 10 минут в день
В противном случае голова будет напрягаться, а ученик начнет совершать глупейшие ошибки. Со временем даже такое «микрообучение» приведет к потрясающим результатам. Нужно лишь набраться терпения и практиковаться согласно рекомендациям математиков.
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Быстрый счет»
Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас
Игра «Математические матрицы»
«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Играть сейчас
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас
Учимся считать во 2 классе
Следующее важное испытание для малыша – поступление во второй класс. Некоторые педагоги следуют выполнению только школьной программы и не оказывают должного внимания процессу обучению своих учеников
Получается так, что ребенок вроде и умеет складывать и вычитать, но в то же время он неспособен понять, почему из одного числа получается другое.
В математике очень важно соблюдать последовательность действий и регулярно тренировать память. Только в таком случае малыш сможет уверенно считать в уме двузначные числа
Если же родители столкнулись с проблемой неуспеваемости их ребенка в школе, педагоги советуют больше заниматься с ним дома. Примеры для домашних занятий:
- Сложить в уме двузначные числа 30+34. Можно предложить малышу разбить 34 на 30 и 4. Так малышу будет проще выполнить сложение. Как можно чаще тренируйте зрительную память при выполнении повседневных дел.
- Выполнить сложение 40+35. Некоторым детям намного легче выполнять сложение в обратную сторону. Для этого нужно округлить меньшее число до ближайшего десятка: 40+40. Затем просто отнять лишнюю часть: 80-5=75.
- Тренируйтесь складывать и вычитать в уме простые примеры. Например: 2+3 или 2+2. Потом начинайте усложнять задачи: 3+7=10, 10-2=8, 10-8=2. Если малыш будет хорошо уметь решать простые задачи, то для него не составят труда задания с двузначными и трехзначными числами.
- Если у ребенка богатая фантазия, можно предложить ему считать предметы или животных в уме. Каждый малыш индивидуален, поэтому родители должны выбрать наиболее подходящую методику обучения, исходя из его особенностей.

Не стоит думать, что желаемый результат будет достигнут быстро, наберитесь терпения. Малышу не так просто обучиться счету, как может показаться на первый взгляд.
Специалисты советуют придерживаться следующих рекомендаций:
- Следить во время занятий, как малыш реагирует на процесс обучения. Если ему скучно и неинтересно, лучше попробовать другую методику.
- Не заставляйте кроху заниматься обучением против его воли. Таким образом вы не добьетесь желаемого результата.
- Не нервничайте во время занятий и не ругайте малыша.
- Регулярно повторяйте уже изученный материал.
- Хвалите малыша за каждое достижение.
Научить ребенка быстро считать не так уж и сложно (рекомендуем прочитать: ). Просто родителям необходимо подойти к этому со всей ответственностью, проявить любовь, терпение и понимание к малышу, тогда результат не заставит себя ждать.
Некоторые родители, едва ли их малышу исполняется хотя бы годик, хотят научить своего ребенка правильно и быстро считать. Другие же не уверены в том, нужно ли этим заниматься с дошкольником, если в школе все равно научат.
Многие специалисты говорят, что делать это нужно лишь тогда, когда малыши проявляют интерес к счету, а не пытаться его навязать. Обычно интерес к счету у малышей проявляется рано, родителям же требуется его подпитать и мотивировать развиваться в этом отношении в форме игр и увлекательных примеров.
Время от времени интерес может угасать, но можно подогревать его
, предлагая вместе посчитать ступени во время ходьбы, игрушки или пуговки на одежде.
Сегодня вы узнаете, как научить ребенка считать, в некоторых случаях это можно сделать быстро, в других случаях потребуется время.
Приемы сложения и вычитания вида□ + 6, 7, 8, 9, □–6, 7, 8, 9
Поселились все зверюшки вместе в теремке. И дружно вместе принялись записывать остальные таблицы. Все примерах в них составляются на основе тех правил, о которых напомнила нам лисичка. Давай поможем им.
Начнем с таблицы сложения числа 6.
В предыдущих таблицах есть только четыре примера, в которых встречается слагаемое 6. Найди их.
Вот что выписали зверята.
Теперь переставляем слагаемые местами.
А теперь из этой таблицы мы легко можем составить таблицу вычитания числа 6. Попробуй сделать это самостоятельно.
Посмотри, какую таблицу вычитания числа 6 записали наши друзья.
Вот мы и закончили! У нас получилось составить таблицы сложения и вычитания числа 6.
Продолжаем. С таблицей сложения числа 7 нам повезло еще больше, ведь в ней будет всего три примера. Ты уже нашел их? Вот что записали зверята.
Надеюсь, ты не забыл еще переместительное свойство действия сложения, ведь оно нам пригодится при составлении таблицы с числом 7.
Подумай над этим сам. А потом проверь.
Все правильно. Теперь из предыдущей таблицы составим таблицу вычитания числа 7.
Не спеши, сделай это самостоятельно.
Проверь свою таблицу.
Как быстро ты со всем справился.
Дальше будет еще легче. Вспомни примеры, где встречается слагаемое 8.
В таблице сложения числа 8 всего два примера. Составь их.
Давай проверим.
Теперь составь таблицу вычитания числа 8.
Вот что получилось у наших друзей.
Вот мы и выучили таблицы сложения и вычитания с числом 8.
Ты, наверное, уже немного устал. Но нам осталось познакомиться всего с одной таблицей. Это таблица сложения и вычитания с числом 9.
Ты уже нашел пример с числом 9? Уверена, что ты справился. Назови его.
9 + 1 = 10
Давай переставлять. Что у нас получится?
1 + 9 = 10
Вот и вся таблица сложения с числом 9. Переходим к таблице вычитания числа 9.
У тебя уже все готово?
Правильно.
10 − 9 = 1
Мы с тобой неплохо потрудились и составили все таблицы в пределах 10. Вот как выглядит общая таблица сложения.
В этой таблице красным цветом выделены примеры, которые составлены путем перестановки слагаемых. Их запомнить очень легко.
А вот общая таблица вычитания чисел в пределах 10.
В этой общей таблице хорошо видны несколько закономерностей, которые помогут тебе лучше и быстрее запомнить результаты указанных математических выражений на вычитание.
- В результате вычитания числа 1 получается число, которое является предыдущим по отношению к уменьшаемому.
- В примерах, где уменьшаемое и вычитаемое являются «соседями» в натуральном ряду чисел, разность равна 1.
- В таблице есть «парные» примеры, которые можно составить из одного и того же примера на сложение.
В этих выражениях компонентами являются одни и те же числа. Присмотрись и найди другие подобные пары примеров.
Чтобы получше запомнить все примеры из таблиц сложения и вычитания чисел в пределах 10, почаще тренируйся. Не забудь о наших сегодняшних помощниках.
Таблицы сложения и вычитания числа 1 мы выучили с помощью мышки, которая переходила маленькими шагами с числа на соседнее число. Как найти результаты в таблицах сложения и вычитания числа 2 нам подсказала лягушка, которая умеет прыгать через число. Зайчик показал, как узнать ответы в примерах из таблиц сложения и вычитания числа 3, который скачет так высоко, что может перепрыгнуть через два числа сразу. А двойной прыжок лягушки поможет вспомнить результаты таблиц сложения и вычитания числа 4. Лисичка же разгадала закономерности составления всех остальных таблиц.
Обязательно используй все приемы, которые нам подсказали герои нашей сказки. Чем чаще ты будешь повторять примеры из таблиц, тем быстрее ты запомнишь результаты каждого из них. Надеюсь, ты легко справишься с проверочными заданиями к этому уроку.
Вычитание и сложение чисел с переходом через десяток
На данном уроке вы вспомните, как складывать и вычитать числа с переходом через десяток. Решая интересные задания, вы повторите алгоритм сложения и вычитания чисел с переходом через десяток. У вас будет возможность попрактиковать изученный ранее материал вместе с веселыми пчелками.
Тема: Повторение
Урок: Вычитание и сложение чисел с переходом через десяток
Посмотрите на числовой ряд. (рис. 1)
Рис. 1
Как связаны пары чисел между собой? В сумме они дают 10.
Запомните эти пары. (рис. 2)
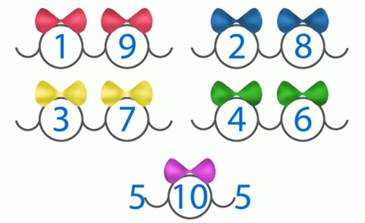
Рис. 2
Это свойство чисел нам пригодится при решении задач.
9 + 6 = ?
Выполним сложение по частям, для этого разбиваем второе слагаемое 6 на две части так, чтобы первая часть дополняла число 9 до десяти. (рис. 3)
Рис. 3
Первая часть – число 1, вторая часть – все что осталось – 5. (рис. 4)
Рис. 4
Значит, 9 + 6 = 15.
1. Читаю пример
Первое слагаемое …
Второе слагаемое …
2. Нахожу число, которое дополнит первое слагаемое до 10. Это число …
3. Разбиваю второе слагаемое на 2 части … и …
4. Дополняю первое слагаемое до 10 и прибавляю оставшиеся единицы. 10 + …
5. Читаю ответ …
Потренируемся в счёте.
Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар. (рис. 5)

Рис. 5
Решение представлено на рисунке. (рис. 6)

Рис. 6
Если у вас возникли затруднения, повторите состав чисел, это вам обязательно поможет.
А теперь рассмотрим пример на вычитание.
11 – 6 = ?
Находим количество единиц в уменьшаемом – число 11 состоит из 1 десятка и 1 единицы. Разбиваем вычитаемое 6 на две части: первая равна количеству единиц уменьшаемого – 1, вторая – оставшихся единиц – 5. (рис. 7)
Рис. 7
Вычитать будем по частям. Вычитаем первую часть: 11 — 1= 10, а потом из 10 вычитаем 5, равно 5. (рис. 8)
Рис. 8
Значит, 11 – 6 = 5
1. Читаю пример
Уменьшаемое …
Вычитаемое …
2. В разряде единиц уменьшаемого число …
3. Разбиваю вычитаемое на две части … и …
4. Вычитаю первую часть …, получаю 10, вычитаю из 10 вторую часть …
5. Читаю ответ.
Закрепим новое знан
Как правильно учить?
Обучение ребенка основам математического счета должно происходить только в игровой форме и при желании малыша. Обучение счету должно вестись в увлекательной игровой форме и непрерывно (каждый день). Задействуется зрительная и тактильная память малыша. Занятия должны быть выстроены в четком алгоритме и иметь систему. Допустим, сначала происходит закрепление понимания “один” и “много”, затем “больше” и “меньше”
Важно объяснить разницу между понятиями “больше”, “меньше”, “равно”. В игровой форме, например, спускаясь по лестнице, научите ребенка порядковому счету от 1 до 10; Покажите ребенку на предметах, как соотносятся произносимые цифры с реальным количеством; Попробуйте на элементарных жизненных ситуациях объяснить ребенку, как происходит увеличение или уменьшение количества предметов, например, к одной машине приехала еще одна, получилось две машины и т.д
Если вы считаете, что формирование такого важного навыка лучше доверить профессионалам, то рекомендуем вам записать ребенка на курсы ментальной арифметики. Результаты занятий вас приятно удивят!