Как научить ребенка делению и умножению столбиком в короткие сроки

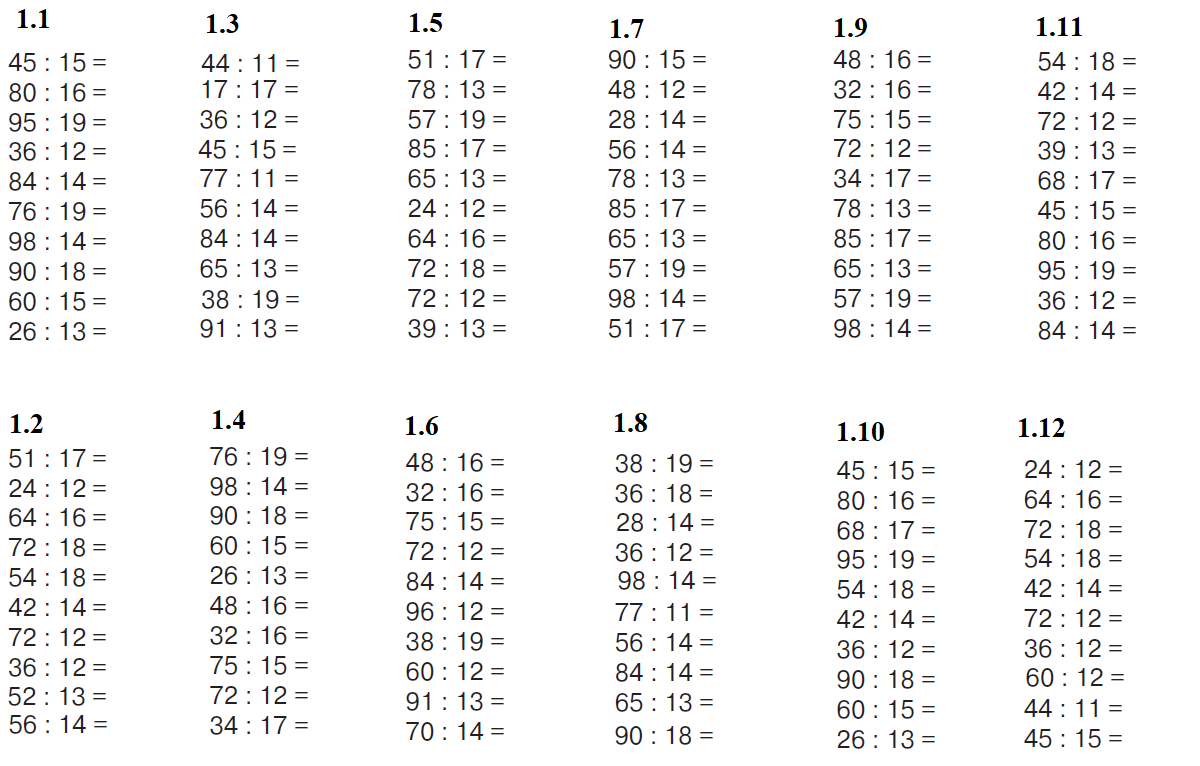
О. Наумова «Учим таблицу умножения. Большой тренажер»

Бесценный богатый тренажер!В книге вы найдете:

110 страниц интересных результативных упражнений;
разнообразные задания;
творческий подход;
нестандартные приемы;
задания разного уровня сложности;
различные шифровки;
игры и раскраски.

Ваш ребенок получит:

легкое и без нервов запоминание таблицы умножения;
развитие внимания и мышления;
улучшение в целом математических способностей;
огромное количество интересных и полезных заданий.

Книга может быть использована как для индивидуальной работы, так и работы в классе.Скучно точно не будет!

Тренажер удобен для распечатывания!

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

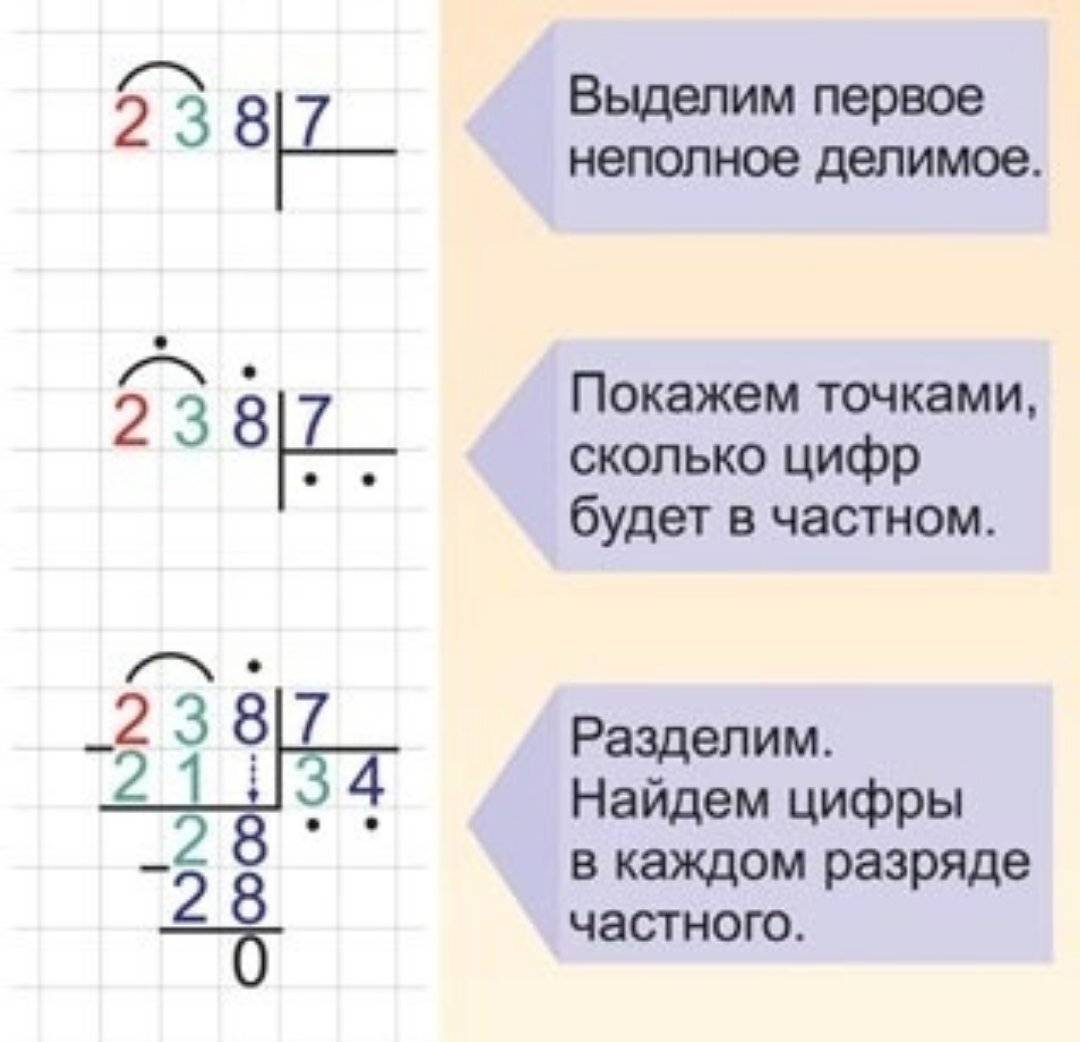
Схематически он выглядит так:

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

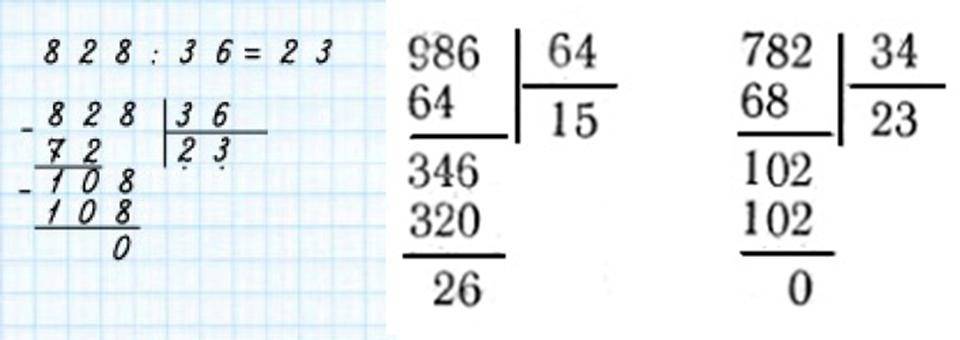
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

Что нужно знать, что бы научиться делить

Математика не любит пропусков. Все знания должны быть крепкими, как кирпичики. Если ребенок не знает основ, с делением будет невероятно трудно

На что следует обратить внимание?

Знает ли школьник название элементов при делении.
Убедитесь, что ребенок не забыл таблицу умножения.
Повторите разряды числа.

Приступаем к делению

Как научить ребенка делить столбиком, мы разберем на конкретных примерах. Следите за рассуждениями и будьте внимательны к цифрам.

Отделяем делимое от делителя скобкой-уголком.

Рассуждаем так: можно ли 4 разделить на 5? Нет, нельзя. Поэтому мы берем не 4, а 46. Вспомним таблицу умножения (можно взять распечатку), какое число в таблице умножения на 5 ближайшее к 46? – 45. Сколько раз 5 помещается в 45? – 9 раз. Подписываем 45 по 46, единицы под единицами, чтобы не запутаться. Девятку пишем «на полочке» – в уголке.

Если от 46 отнять 45, сколько получим? -1. Один меньше пяти? – меньше. Значит, мы разделили правильно.

Один на 5 не делится, сносим оставшееся число – 5, получаем 15. Пятнадцать делится на пять? — делится. Сколько получается? – 3. Тройку записываем в уголке. Проверяем решение: три умножить на 5, будет 15. Подписываем его под предыдущим числом. Из пятнадцати вычесть пятнадцать – будет ноль. Мы использовали все числа из делимого, значит, решили пример правильно.

В уголке мы записали две цифры – 9 и 3, получили число 93. Девяносто три – это частное, которое является решением нашего примера.

Объясняя школьнику, как научиться делить столбиком, выполняйте проверку обратным действием: 93*5. Кроме того, решайте более сложные варианты.

Есть и другие, частные случаи – о них Вы узнаете из программы. Если в учебнике действительно «ничего нет», возьмите за правило сверять решение с классной работой. Из классной тетрадки легко понять, каким методом пользуется учитель, и повторить его при объяснении домашней работы.

Как научиться делить в столбик с остатком

Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.

Для примера разделим 235 на 14.

235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.

К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Методом подбора разделим 90 : 10 = 9, но в нашем случае 14 х 9= 126, что больше 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.

Во время решения примеров с остатком, ответ может быть записан двумя способами:

в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
но чаще всего ответ записывают словами: 6 целых и 11 в остатке.

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук

Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

При умножении любого числа на 1 получается то число, которое умножали.
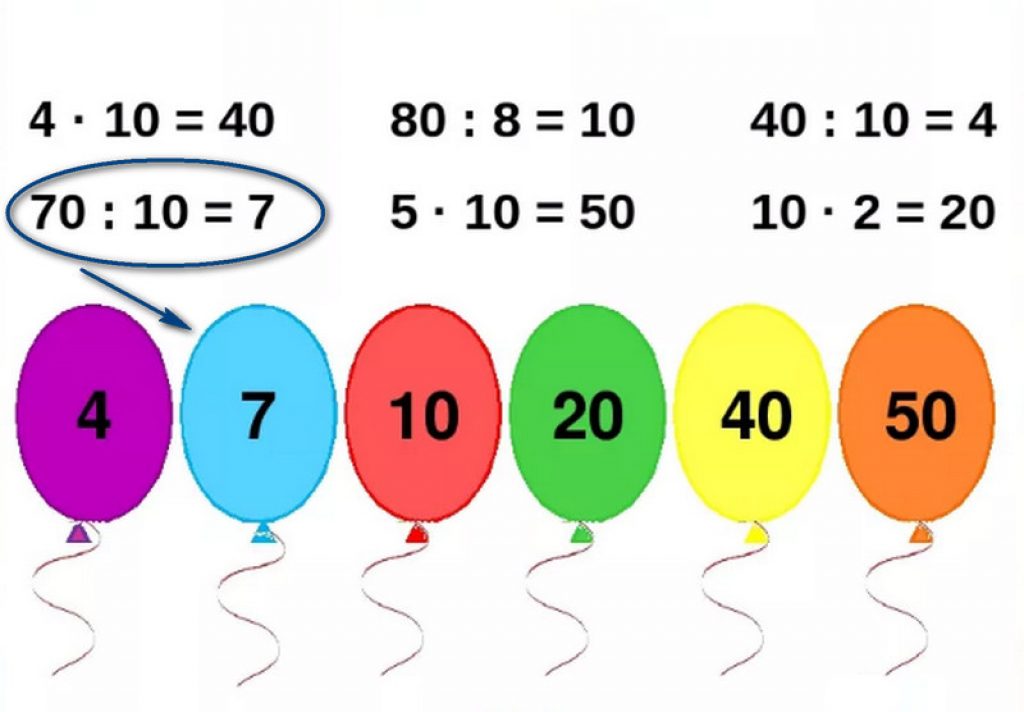
Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.

Научиться пользоваться таблицей Пифагора

Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.

Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).

Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.

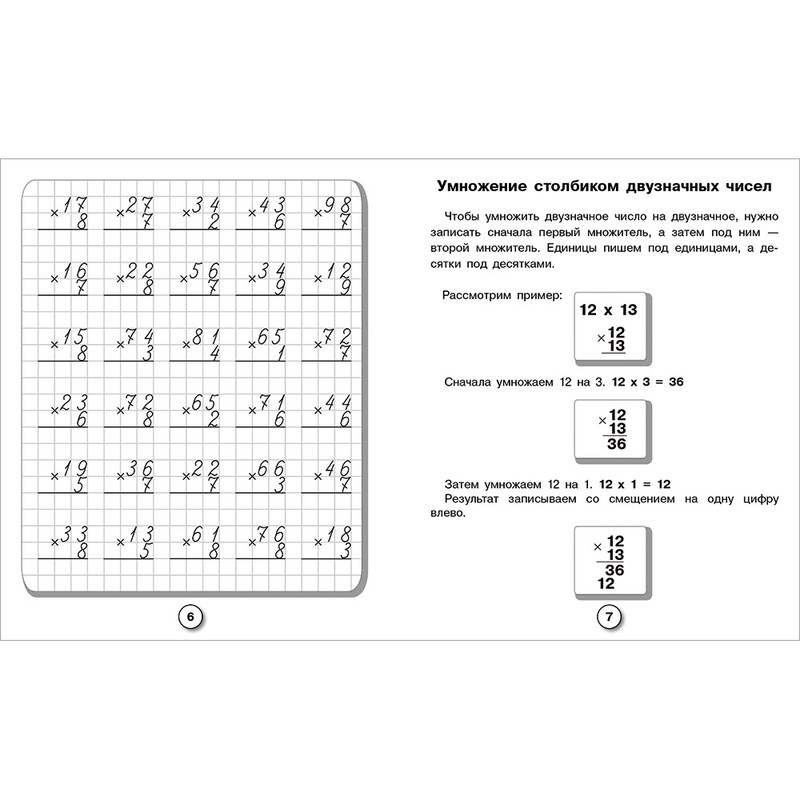
Как умножать столбиком? Как объяснить ребенку умножение столбиком? Умножение на однозначное число, двузначное число, трехзначное число: алгоритм умножения чисел

Ребенка просто научить умножать столбиком, если делать это в игровой форме.

Математика — это сложная наука почти для каждого ребенка

Родителям приходится заставлять своего чада выполнять домашние задания, ведь это необходимо не только для получения хороших оценок в школе, но и для развития
Напряженная работа мозга помогает развить память, интеллект, внимание и приобрести отличные навыки счета
Все качества, приобретенные в школе, будут полезными в будущей жизни. Считать нужно уметь не только ученым, но и рабочим, и домохозяйкам

Одно из самых сложных действий — это умножение. Оно дается сразу не каждому ребенку

Как объяснить ребенку умножение столбиком?

Научить ребенка умножению — это реальная задача, но придется запастись терпением. Занятие должны быть регулярными, ведь только система поможет добиться желаемых результатов.

Расскажите ребенку, что умножение — это повторение, сложение одинаковых чисел
Напишите на листе бумаги примеры: 2+2+2+2+2 и 2х5
Сделайте вместе с ребенком сравнение, как быстрее подсчитать сложением или умножением
Чтобы закрепить эту полученную информацию, приведите примеры из жизни, но они должны быть не выдуманными. Например, к ребенку в гости идут 7 друзей. Для них готово лакомство — по 2 конфеты. Как быстрее подсчитать — сложением или умножением? Подсчитайте вместе с малышом и запишите на бумаге в виде примера: 7х2=14

Когда пройдет несколько занятий, таблица умножения будет выучена, тогда можно начинать объяснять ребенку умножение столбиком двухзначных и трехзначных чисел.

Умножение на однозначное число

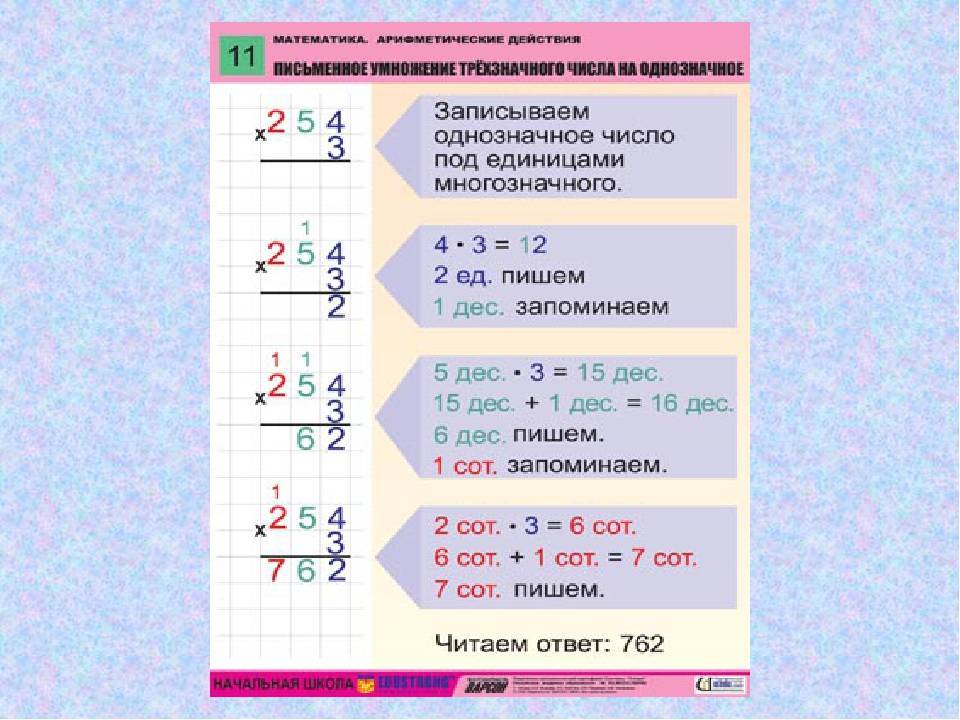
Дети уже в третьем классе начинают проходить умножение в столбик на двухзначные и трехзначные числа. Но сначала необходимо объяснить умножение на однозначное число, например, 76х3:

Сначала умножаем 3 на 6, получается 18 — 1 десяток и восемь единиц, 8 единиц пишем, а 1 запоминаем. Единицу мы потом будем прибавлять к десяткам
Теперь умножаем 3 на 7, получается 21 десяток + единица, которую запоминали, получилось 22 десятка
Используем правило умножения в столбик: последнюю цифру оставляем, а ниже записываем десятки, получилось 228

Умножение на двузначное число

Двух-, трех-, четырехзначные числа можно умножить на однозначные в уме. Когда ребенок станет немного старше, он так и будет делать. Но умножать на двухзначное число в уме ему еще сложно. Поэтому применяется снова действие в столбик.

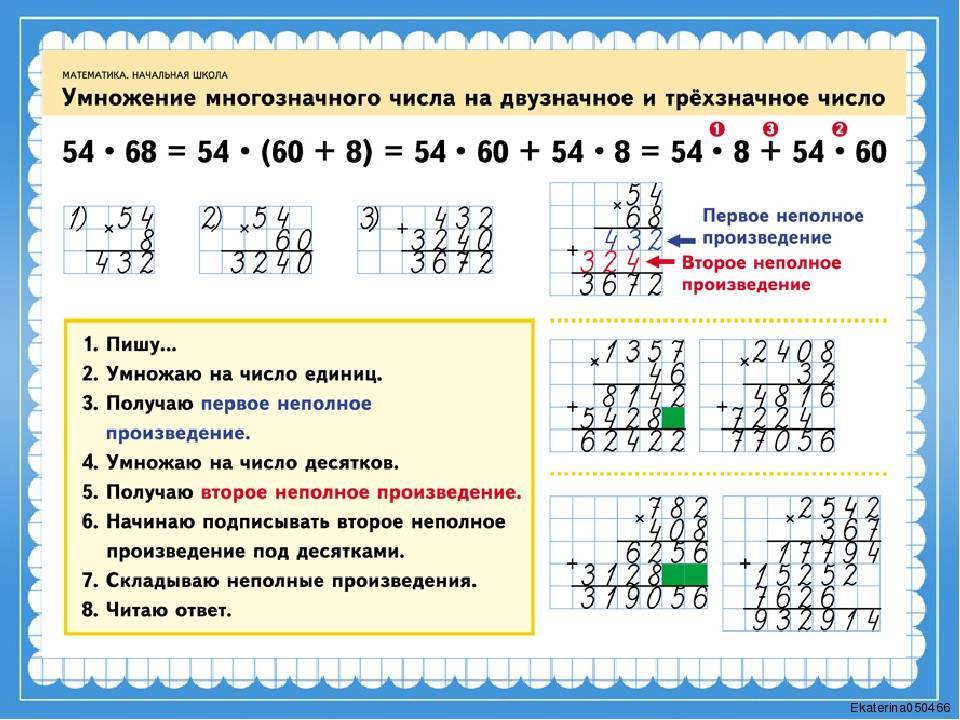
Пример: Делаем умножение на двузначное число — 45х75:

Под числом 45 записываем 75 по правилу: единицы под единицами, десятки под десятками
Умножение начинаем делать с единиц: 25 — 5 пишем, 2 запоминаем, чтобы потом прибавить к десяткам
Умножаем 5 на 4, получается 20. Прибавляем к десяткам 2, получается 22. Записываем впереди цифры 5, получается 225
7х5=35. Цифру 5 записываем под десятками, 3 запоминаем и будем ее записывать потом в сотни
7х4=28 сотен. Прибавляем 3, получается 31 сотня. Записываем по правилу умножения в столбик
Складываем неполные произведения — единицы, десятки и сотни и получаем результат: 45х75=3375

Умножение на трехзначное число

Есть такие люди, которые производят умножение трехзначных чисел в уме. Ребенку, естественно, сложно это делать, поэтому он должен оттачивать навыки на бумаге.

Умножение на трехзначное число производится по такому же принципу, как и умножение на двухзначное число:

Сначала умножаются единицы и записываются в строку
Ниже будут записаны десятки по правилу умножения в столбик
Третьей строкой записывается произведение сотен
В итоге получатся тысячи, сотни, десятки и единицы, которые нужно сложить

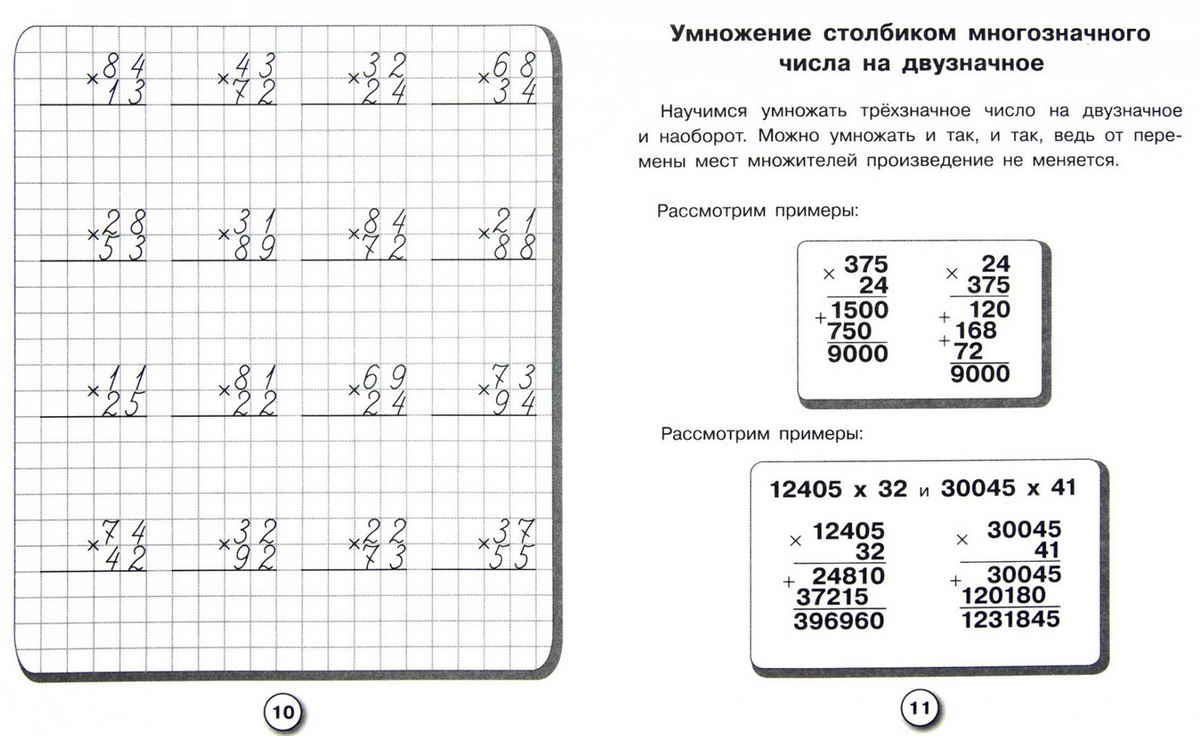
Как умножать столбиком двузначные числа?

Как умножать столбиком двузначные числа

Как умножать столбиком двузначные числа мы рассмотрели выше, а как умножить большое число на двузначное следует разобрать подробнее:

Пример: 4325х23

Сначала умножаем 3 на 5, на 2, на 3 и на 4. Записываем единицы, десятки, сотни и тысячи
Теперь умножаем 2 на 5, на 2, на 3 и на 4. Также записываем, но уже десятки под десятками, сотни под сотнями, а тысячи под тысячами
Складываем по правилу и получаем результат: 4325х23=99475

Алгоритм умножения чисел

Алгоритм умножения чисел заключается в применении таблицы умножения. Поэтому ребенок сначала должен досконально выучить таблицу умножения, а потом учиться выполнять действие со сложными числами.

Игры на умножение

Игры на умножение:

Ребенку будет легче запомнить таблицу умножения в стихотворной форме, а занимательный персонаж поможет ему в этом.

«Магическая» таблица Пифагора

Положите перед собой лист с распечатанной таблицей Пифагора. Выглядит она так:

Пифагорова таблица имеет более упрощенную форму, чем таблица с примерами в столбец. Она не содержит лишней информации, которая только путает и усложняет запоминание.

Чтобы ребенок понял принцип умножения<, попробуйте для начала объяснить его на простом примере.

2 × 3 — аналогично действию 2 + 2 + 2, то есть сложить число 2 три раза.

Покажите, как работает таблица: число на месте пересечения столбца и верхней строки – это и есть правильный ответ. Малышу нужно запомнить только 36 комбинаций. Остальные действия – повторяются или очень легкие.

Видео-материалы по теме статьи

Учим таблицу умножения (способ с монетками):

Как быстро выучить таблицу умножения:

Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению. Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс

Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее

Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.

Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.

Вместе с этим ищут и читают:

Теперь вам необходимо решить, как научить ребенка делить. Если он уже перешел в третий класс, трудностей у вас возникнуть не должно. Для начала объясните малышу зависимость между делением и умножением. Продемонстрируйте ему, как правильно делить столбиком, используя таблицу умножения. Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.

Объясните ученику, который перешел в третий класс, что категории, описывающие деление, называются «делимое», «делитель», «частное». Продемонстрируйте это наглядно с помощью таблицы. Рассмотрите как можно больше примеров, чтобы малышу было понятнее. Это пригодится в дальнейшем, когда вы будете осваивать деление столбиком. По сути, вам необходимо научить кроху смотреть на таблицу умножения «наоборот».

Перед началом занятий еще раз вспомните категории деления. Теперь попробуем объяснить все наглядно. Например, разделим число девятьсот тридцать восемь на семь. Запишем числа, чтобы делить их столбиком. Если вы только начинаете обучение, то ребенку, который пошел в третий класс, будет проще для начала делить числа без остатка. Теперь показываем ученику числа делимого и предлагаем ему выбрать наименьшее число, которое будет больше, чем делитель. Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.

Умножаем семь на один, получаем семь. Этот результат мы записываем под девяткой из числа девятьсот тридцать восемь. Вычитаем от девятки семерку в столбик. В остатке получаем два. Аналогичным образом записываем результат. Полученное число меньше, чем делитель. Таким образом, нам необходимо его увеличить. Объединяем его со следующим неиспользованным числом – тройкой. «Плюсуем» тройку и двойку. Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.

Самое главное в процессе обучения малыша, который перешел в третий класс, чтобы он усвоил простой алгоритм. Развивайте наблюдательность у крохи, проводите аналогии с другими математическими действиями, больше играйте и наблюдайте за природой.

В классе много детей, и у учителя не всегда получается уделить внимание каждому. Однако если ребенок что-то пропустит или не поймет, то это затруднит изучение дальнейших тем

В этом случае на помощь ему должны прийти родители. К примеру, как научить ребенка делению? Сначала математический процесс лучше объяснять в игровой форме. Затем можно переходить к более сложным задачам.

Умножение в столбик на двузначное число

Представим, что нам нужно умножить 4235 на 86. Для этого сначала записываем первый множитель:

Теперь записываем второй множитель так, чтобы единицы второго множителя оказались под единицами первого, а десятки второго – под десятками первого:

Далее ставим знак «х» и подводим черту:

Начинаем умножать. Сначала умножаем 4235 на 6 и получаем 25410:

Затем умножаем 4235 на 8 десятков и получаем 33880. Это число записываем под первым и ставим вместо знака «х» знак «+»:

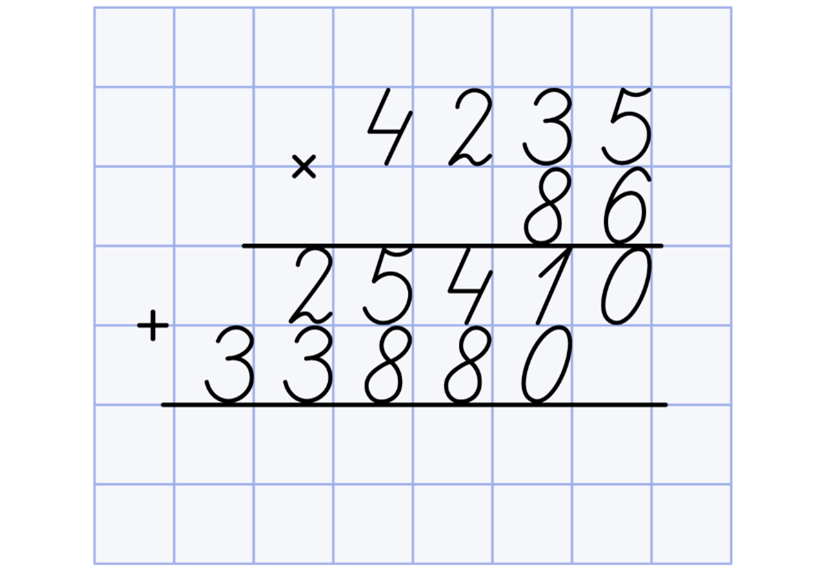
После сложения получаем 364210:

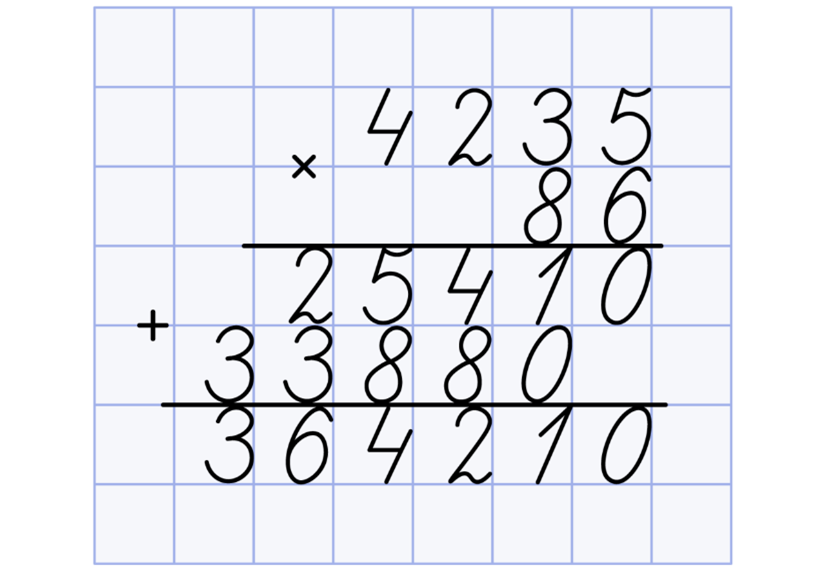
Таким образом, получаем простой алгоритм умножения столбиком на двузначное число:

Записываете первый множитель.
Записываете второй множитель, чтобы его единицы оказались под единицами первого, а десятки – под десятками.
Ставите знак «х» и подводите внизу черту.
Умножаете первый множитель на единицы второго. Результат записываете под чертой.
Умножаете первый множитель на десятки второго. Результат записываете под предыдущим результатом. Слева ставите знак «+».
Складываете полученные числа.
Получаете ответ.

В случае, когда второй множитель оканчивается на ноль, запись производится иначе: второй множитель нужно записать так, чтобы цифра, отличная от нуля, оказалась под единицами второго множителя.

К примеру, вам надо умножить 937 на 50. Сначала записываете так:

Далее 937 умножаете на 5:

После этого к полученному результату дописываете столько нулей, сколько их оказалось справа во втором множителе:

Когда оба множителя заканчиваются нулями, запись снова делается иначе: два множителя нужно записать, чтобы крайние справа цифры, отличные от нуля, оказались друг под другом.

Допустим, вам требуется умножить 72400 на 30. Сначала записываете так:

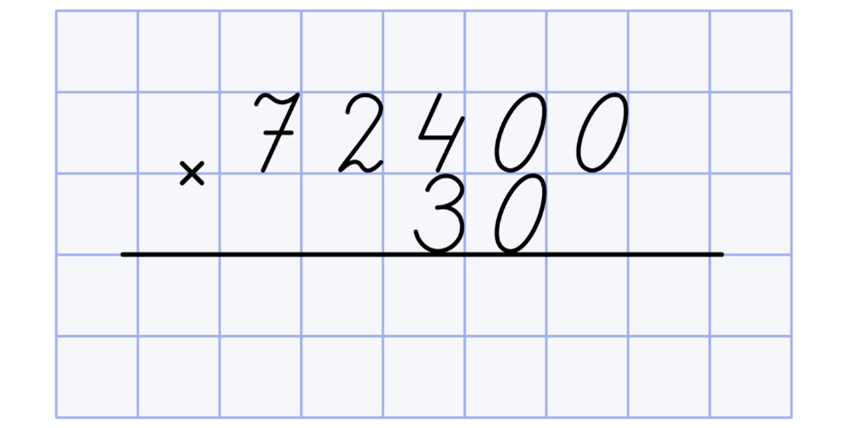
Выполните умножение, не беря нули во внимание:

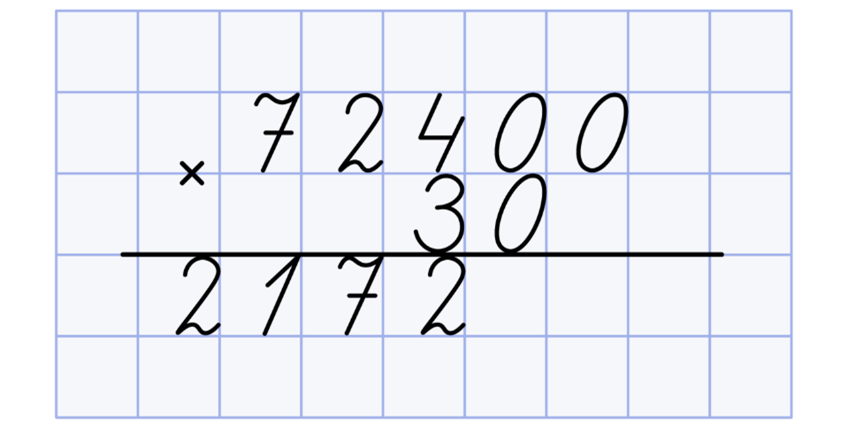
После этого запишите в ответ столько нулей, сколько их оказалось справа в обоих множителях:

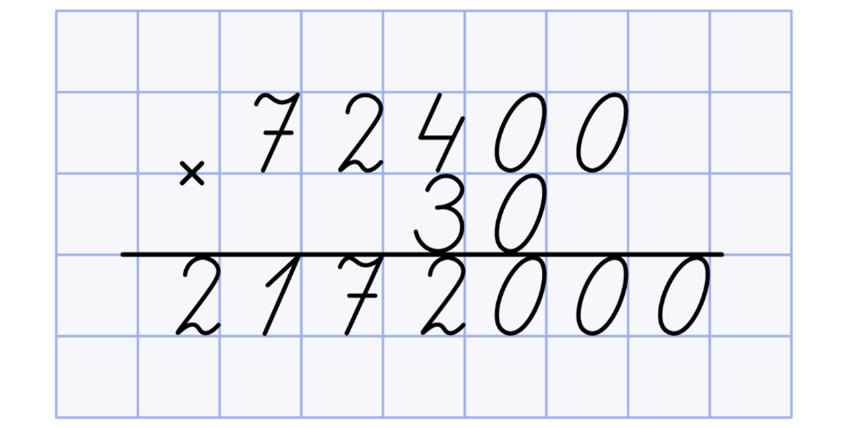
И, наконец, осталось узнать, как умножать столбиком на трехзначное число.

Обучаемся операции по делению на части

На данном этапе лучше сформировать понимание того, что главное в процессе деления, это разделение чего-то на равные части. Самым простым способом научиться этому для ребенка, это будет предложить ему поделить несколько предметов между ним и членами семьи или друзьями.

К примеру, возьмите 6 одинаковых предметов и предложите ребенку поделить их на две равные части. Можно немного усложнить задание, предложив поделить не на две, а на три равные части.

Важным моментом здесь считается проводить операции по делению четных количеств предметов. Такое действие окажется полезным на дальнейшем этапе, когда ребенку будет необходимо понимание того, что разделение, это действие, обратное умножению.

Делим и умножаем, при помощи таблицы умножения

Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.

Например
: 2 умножить на 4 будет восемь

Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения

Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.

Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное»

Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!

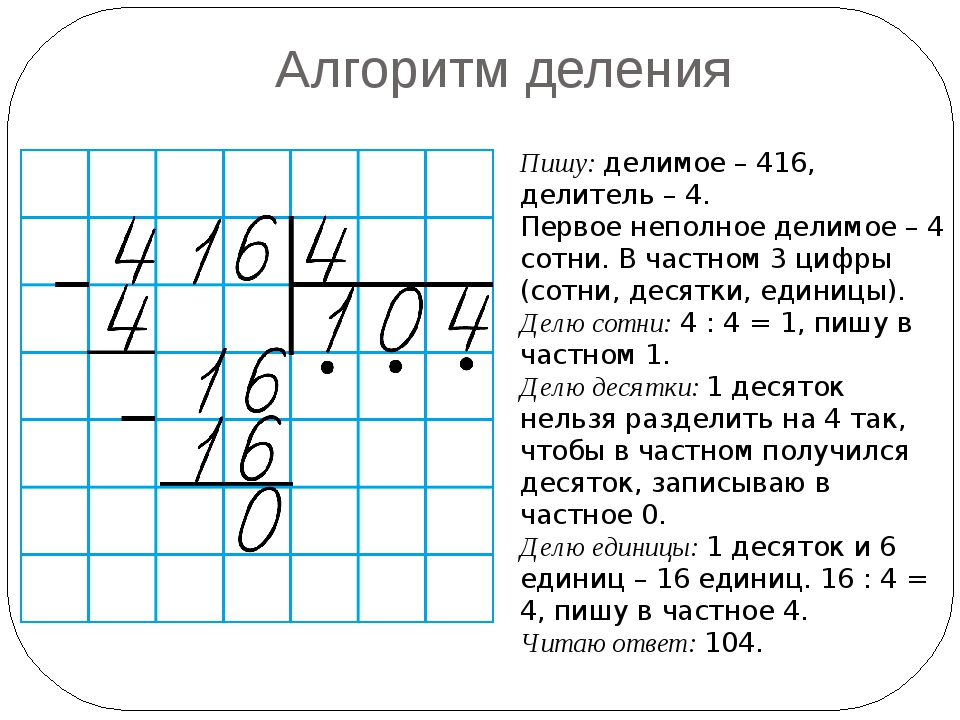
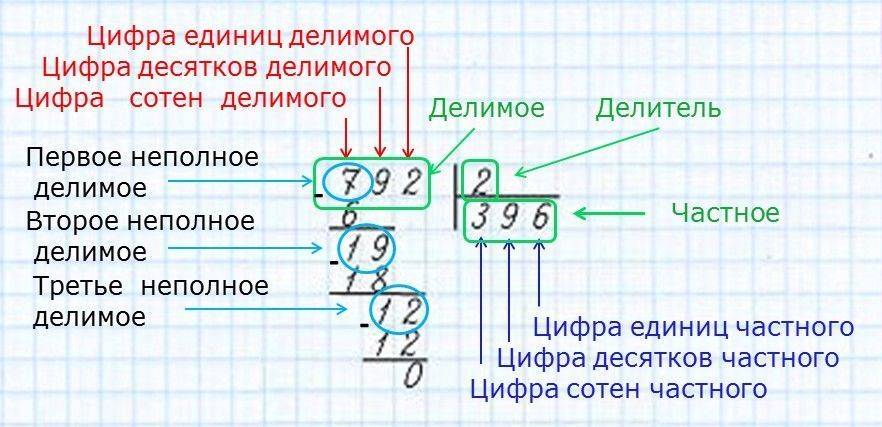
Делить в столбик трёхзначное число на однозначное

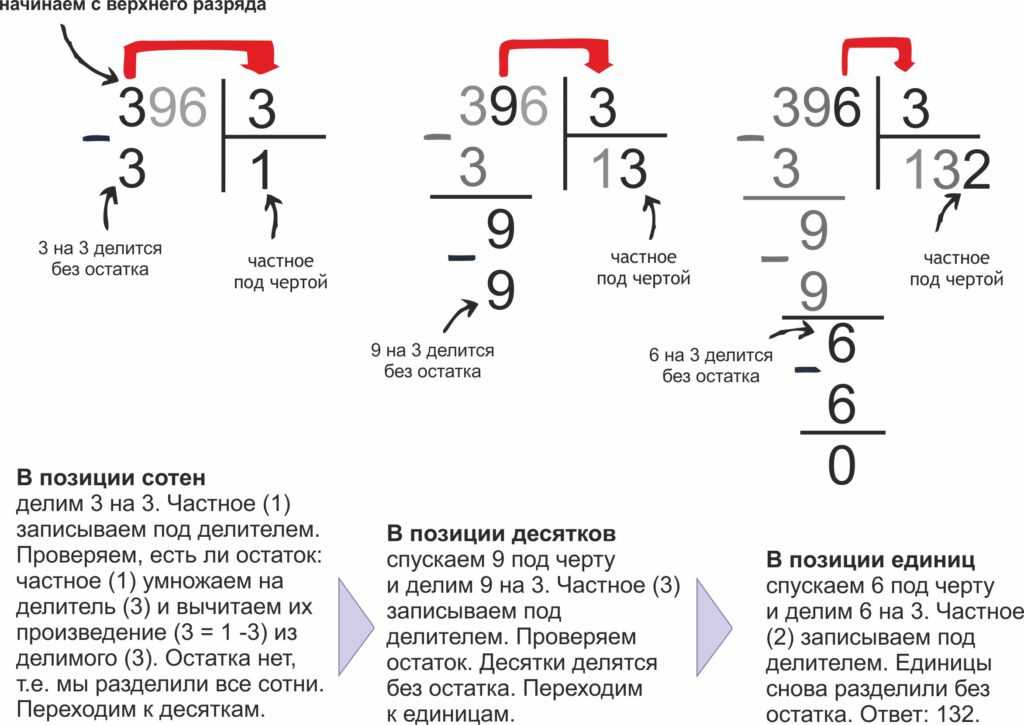
Разделим 486 на 3

1. Сначала определим, сколько цифр в частном: первая цифра делимого — 4, мы можем разделить 4 на 3, значит, в частном будет первая цифра. После первого неполного делимого ещё две цифры, значит, и в частном будет ещё две цифры — всего три.

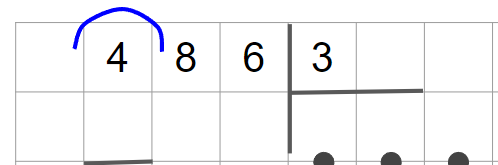
2. Затем разделим первое неполное делимое 4 на делитель 3. В результате получим 1.

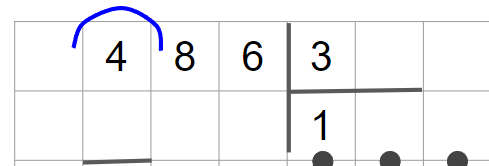
3. Далее умножим делитель на полученную цифру частного: 3 · 1 = 3. Запишем 3 под первым неполным делителем.

4. Теперь нужно найти остаток при помощи вычитания.

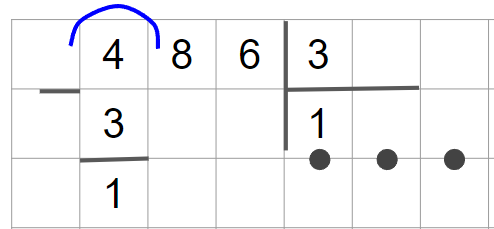
5. Остаток 1 меньше делителя 3, значит, продолжаем вычисления. Рядом с цифрой остатка 1 пишем следующую цифру делимого — 8. Следующее неполное делимое — 18.

6. Разделим 18 на 3 и получим вторую цифру частного — 6.

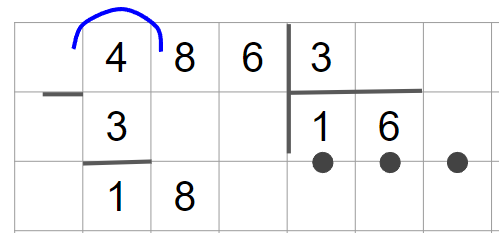
7. Теперь умножим делитель на полученную цифру частного: 3 · 6 = 18 и найдём остаток — 0. Его можно не писать.

8. Сносим цифру 6 — это последнее неполное делимое. Делим 6 на 3 и получаем — 2. В частное пишем 2.

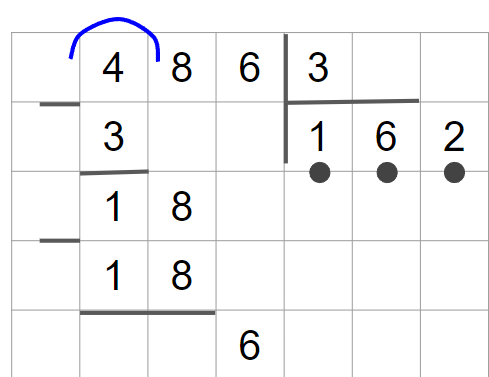
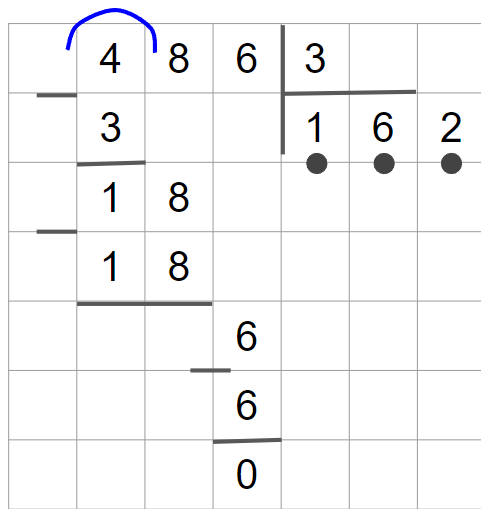
9. Далее умножим делитель на полученную цифру частного: 3 · 2 = 6 и найдём остаток — 0. Вычисления закончены.

Читайте по теме:

Основные единицы измерения в начальной школе

ВЫЧИСЛЕНИЯ С ДРОБЯМИ, СТЕПЕНЯМИ И СЛОЖНЫМИ ФУНКЦИЯМИ

Это сложные расчетные случаи, которые не изучаются в начальной школе.

Умножение простых дробей друг на друга не кажется сложным. Просто умножьте числитель на числитель и знаменатель на знаменатель. Пример.

Разделить первую дробь не так сложно, как может показаться. Все, что вам нужно сделать, это превратить задачу в пример на умножение. Это легко сделать. Поверните дроби так, чтобы знаменатель стал числителем, а числитель — знаменателем. Пример.

Если в задаче есть число в виде силы, то это значение вычисляется раньше всех остальных (вы можете представить его в скобках — действие в скобках выполняется первым). Пример.

Решение примера было простым: преобразование числа, выраженного в виде мощности, в регулярное выражение с помощью действия multiply. Сначала умножение, потом вычитание (потому что оно в скобках), а затем деление.

Такие функции изучаются только в средней школе и поэтому не рассматриваются. Как и в случае с полномочиями, они имеют приоритет при расчете. Сначала находится значение выражения, затем выполняется обычная серия вычислений. -прозрачные строчки, умножение на деление, затем слева направо.

Как делить столбиком десятичные дроби с запятой?

Существует несколько особенностей при подобном делении. Если вы совершаете действие с:

десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.

Действие умножения

Если понимать, что умножение – это сложение одинаковых чисел определенное количество раз, ничего сложного в действии нет. Например, 4*7 = 4+4+4+4+4+4+4. В итоге получают 28. Упростит действие таблица умножения. Ее знает каждый школьник.

Чтобы правильно умножать числа, их сводят к простым. Рассмотрим техники умножения.

Умножение 9 и 11

Правило при умножении на 9 умножают на 10 и вычитают 9. Если умножают на 11, сначала умножают на 10, прибавляя исходный показатель.

Пример:

15*9 = 15*10-15 = 150-15 = 135;
57*11 = 57*10+57 = 570+57 = 627.

Умножение на 5 чисел до 10

Эта техника поможет правильно умножать двух-, трехзначные числа. Правило простое – множитель делят на 2. Получив результат в виде целого показателя, добавляют в конце 0, а если число не целое, отбрасывают остаток и добавляют в конце 5.

Пример 1482*5 решают так:

(1482/2) _ (+0 или +5) = 741 _ (+0) = 7410 – исходный показатель делили на 2 без остатка;
2269-5 = (2269/2) _ (+0 или +5) = 1134,5 _ (+5) = 11345 – исходный показатель делили на 2 с остатком.

Техника, как быстро научиться считать деньги, умножая число на 5, 25, 50, 125 с использованием формул:

А*5 = А*10/2;
А*50 = А*100/2;
А*25 = А*100/4;
А*125 = А*1000/8.

Приставляя вместо А цифру, в процессе решения формулы получают нужный результат. Например, 25*25 = 25*100/4 = 2500/4 = 625.

Умножение больших чисел с одним четным

В этом случае пользуются методикой упрощения множителей. Четное число уменьшают в 2 раза, а нечетное увеличивают в 2 раза. Например, 48*125 = 24*250 = 12*500 = 6*1000 = 6000.

Умножение многозначного числа на однозначное

Разбираясь, как научиться быстро считать деньги на кассе, пользуются техникой раскладывания на порядки, как в случае сложения. Пример 468*6 решают так:

Раскладывают 468 на 400, 60, 8. Умножают каждое число на 6.
Получают (400*6) = 2400 + (60*6) = 360 + (8*6) = 48. Итого 2400+360+48 = 2808.

Более сложный вариант с перегруппировкой итоговых результатов выглядит так: 2400+360+48 = 2000+400+300+60+48 = 2000+700+108 = 2808.

Умножение простых чисел

Диагональный метод нужен при поисках техники как быстро научиться считать устно. Заключается способ в дописывании числа, которого «не хватает до 10».

Пример 7*8 решают так:

высчитают недостающее до 10 – в 7 это 3, в 8 это 2;
затем 8-3 = 5;
3*2 = 6;
в итоге получают 56.

Умножение чисел от 10 до 20

Правило – к одному числу прибавляют единицы другого, а сумму умножают 10. К результату добавляют сумму единиц. Например, 13*15 = (13+5)*10 + 3*5 = 180+15 = 195.

Умножение двузначных чисел

Упрощают процесс снова разложением двузначных чисел на простые действия. Пример 78*56 решают так:

В итоге должно получиться сложение цифры 78 точно 56 раз. Сначала складывают 78 пятьдесят раз, затем еще 6 раз.
Считают 78*5 = 70*5 + 8*5 = 350+40 = 390*10 = 3900.
78*6 = 70*6 + 8*6 = 420+48 = 468.
3900+468 = 3000+900+400+60+8 = (3000+1300+60+8) = 4368.

Пользуясь принципом упрощения и раскладывания больших чисел на разряды, умножают все двузначные числа.

Умножение на 9, 99, 999

Учитывают правило прибавления недостающих единиц. Пример 154*99 решают так: 154*(100-1) = 15400-154 = 15246. Таким же образом умножают на 9, 999.

Возведение в квадрат

Это тоже умножение, при котором число раскладывают на составляющие. Сначала находят произведение первой цифры на следующую за ней, результат будет заканчиваться на квадрат последней цифры. Пример возведения 75 в квадрат решают так: 7*8 = 56; 5*5 = 25. В итоге 75*75 = 5625.

Умножение чисел

При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

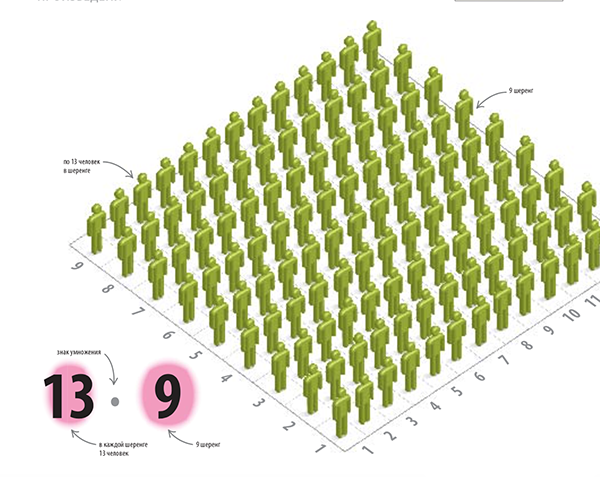
Иллюстрация из книги «Как объяснить ребенку математику»

Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.

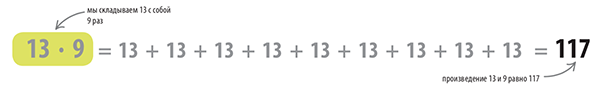
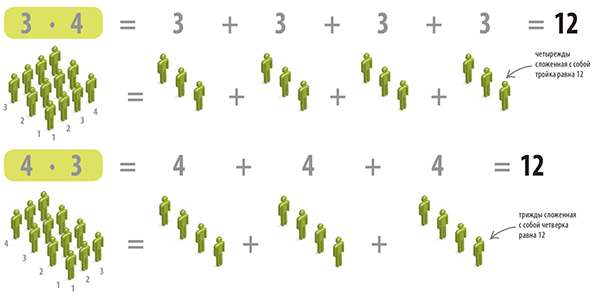
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.

Некоторые числа легко умножать, зная особые приемы. Вот они.

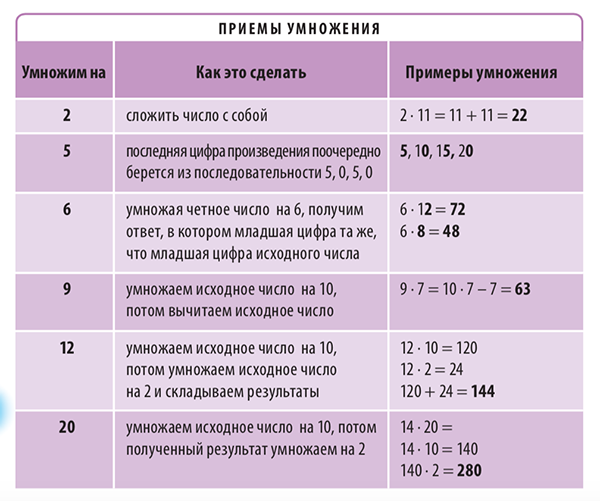
Таблица из книги «Как объяснить ребенку математику»

В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

❓Вопросы и ответы

А также вот несколько ответов на часто задаваемые вопросы.

Почему умножение называют повторным прибавлением?

Умножение представляет собой вариацию повторяющегося прибавления числа. Именно поэтому его называют повторным или многократным прибавлением, что зависит от того, на сколько нужно умножить первое число.

Почему нельзя умножать на ноль?

Умножать на ноль можно, но его особенность при умножении такова, что, если в примере фигурирует ноль как самостоятельное число, ответ всегда будет равен нулю.

Какие еще есть арифметические операции?

Кроме умножения есть еще несколько элементарных арифметических операций. Ими являются сложение, вычитание и деление.

Еще одни факты в обучении

Умножение ( х )- это коммутативная операция. Это означает, что вы можете изменить порядок чисел, и ответ будет таким же. Так например:

8 х 6 = 48 и
6 х 8 = 48

Хитрости в обучении таблицы умножения на 9

Все знают таблицу умножения на 10, но есть хитрость как узнать таблицу умножения на 9

Продолжая тему «разделяй и властвуй», мы можем покорить таблицу (х ) на девять и десять. Я полагаю, что каждый знает свою таблицу (х ) на девять, и большинство людей знают трюк, чтобы выучить таблицу умножения на девять.

Если вы не знаете трюка с таблицей (х ) на девять, вы можете выбрать из числа. Некоторые включают в себя очень простые вычисления в уме, другие заставляют вас использовать пальцы. Лучше всего выбрать трюк, который вам подходит. Просто погуглите «девятикратный трюк» и выберите свой любимый. Если вы потратите время, чтобы просмотреть один или два примера и сделать выбор, этот опят останется неизменным.

Как умножать в столбик

Все мы изучали в школе методы выполнения арифметических операций над числами. Чтобы облегчить процесс счета и ускорить его в разные времена для этого применялись различные устройства. Старшее поколение возможно еще помнит счеты и логарифмическую линейку, в то время как молодым известен только электронный калькулятор в различных его проявлениях.

Тем не менее, есть еще один универсальный способ выполнения арифметических операций без использования вспомогательных устройств известный всем с детства, это выполнения операций в столбик на листе бумаги. Мы уже рассматривали ранее сложение, вычитание и деление, а сейчас давай освежим нашу память и вспомним, как выполняется умножение в столбик.

Чтобы перемножить два числа в столбик (например 381 на 29), их нужно записать одно под другим, удобнее большее число располагается над меньшим.

После этого проводим под ними горизонтальную черту и пишем слева от них знак умножения «×».

Подготовительные операции выполнены, теперь переходим непосредственно к процессу перемножения. Счет идет справа налево, берем разряд единиц двух множителей в данном примере 1 и 9 и перемножаем их воспользовавшись знанием таблицы умножения. У нас получается 9, поскольку получившееся число меньше 10, то оно просто записывается под чертой в разряде единиц.

Теперь нам нужно перемножить цифру из разряда единиц нижнего числа на цифру из разряда десятков верхнего, то есть 9 на 8.

Разряд единиц записывается под чертой левее ранее записанной цифры, то есть в разряде десятков, а 7 пишем над нашим столбиком, но со смещением на одну позицию вправо, над сотнями.

Следующим шагом нужно перемножить разряд единиц нижнего числа с разрядом сотен верхнего 9 на 3.

Таблица умножения подсказывает, что в результате получится 27, но наверху над сотнями у нас еще записана цифра 7, значит ее нужно прибавить к 27 и в результате получится 34.

Половину дела мы сделали, перемножили 9 из нижнего множителя со всеми цифрами из верхнего. Теперь нужно сделать то же самое со второй цифрой из нижнего числа. Для этого считаем 2×1=2. Результат меньше 9, значит просто записываем его под чертой в столбце десятков, но уже на строчку ниже.

Следуя алгоритму, находим произведение чисел 2 и 8, в результате получается 16. Поскольку он больше 9, то он разбивается на две части, 6 записываем в столбце сотен под чертой, а 1 наверху столбика. Поскольку там уже есть 7 от предыдущего шага вычислений, то зачеркиваем ее, чтобы не запутаться.

Остался последний шаг, вычисляем 2×3=6 и наверху есть цифра 1, значит 6+1=7. Поскольку 7 меньше 10, то записываем ее под чертой левее предыдущей.

Единственное что нужно отметить это то, что в позиции ниже 9 и правее 2 находится 0, который мы не записали.

В результате мы нашли произведение двух чисел методом умножения в столбик и получили результат 11049. Кажется все очень сложно, но на самом деле долго объяснять, а когда дело доходит до практических вычислений все оказывается довольно быстро.

Фактически данный способ сводится к разбиению одного из множителей на составляющие его цифры, перемножение этих чисел с другим множителем и умножении получившегося числа на соответствующий разряд, а затем сложение получившихся чисел.

С тем же успехом можно было сделать наоборот, 1×29×1=29, 8×29×10=2320, 3×29×100=8700. Теперь считаем 29+2320+8700=11049, результат тот же, надеюсь это никого не удивляет.

Умение выполнять арифметические операции без помощи калькулятора может сослужить хорошую службу даже в наш век повсеместного использования компьютеров. Впрочем, пересчитывать единицы информации все таки гораздо проще в онлайн-конвертере.

Как обучить ребенка делить и умножать числа