Понимание эффекта мультипликатора
Как правило, экономистов больше всего интересует, как вливания капитала положительно влияют на доход. Большинство экономистов считают, что вливание капитала любого вида – будь то на правительственном или корпоративном уровне – окажет широкий эффект снежного кома на различные аспекты экономической деятельности.
Как следует из названия, эффект мультипликатора дает численное значение или оценку ожидаемого увеличения дохода на доллар инвестиций. Как правило, множитель, используемый при оценке эффекта мультипликатора, рассчитывается следующим образом:
Мультипликатор = Изменение в доходах / Изменение в расходах
Эффект мультипликатора можно увидеть в нескольких различных типах сценариев и использовать различные аналитики при анализе и оценке ожиданий в отношении новых капитальных вложений.
Личная жизнь
Затворнический образ жизни оставляет сотни вопросов. Главный, интересующий журналистов и граждан, – это причина, по которой Григорий Перельман отказался от по праву принадлежащих ему денег. Речь идет о премии института Клэя. Математический институт составил список семи загадок, за решение которых полагается награда в миллион долларов. Гипотеза Пуанкаре входила в данный список.
Григорий Перельман и его мама
Разумеется, узнав об открытии российского ученого, учредители незамедлительно обратились к ученому. Каково же было всеобщее удивление, когда математик отказался от миллиона долларов без объяснения причин.
Вскоре Григорий Яковлевич вовсе перестал общаться с прессой. Российских журналистов попросту игнорирует, а зарубежным отказывает в интервью. Новости о подобном поведении ученого повлекли за собой слухи о болезни Перельмана. Утверждали, что гений страдает аутизмом. Впрочем, достоверных подтверждений или заключений врачей до сих пор не обнародовано.
Как использовать эффект Розенталя во благо себе? 3 главных совета
Чтобы надежно защититься от негативных эффектов «самосбывающегося пророчества» и использовать феномен себе на пользу, стоит следовать простым и надежным советам:
1. Избегайте негативных ожиданий и работайте над ними
В работе и жизни старайтесь концентрировать свое внимание именно на положительных вариантах развития событий. Если же вас посещают тревожные мысли – работайте с ними, заранее продумывайте способ выхода из ситуации
Например:
2. Формируйте внутреннюю референцию и остерегайтесь поспешных выводов
В психологии разделяют два типа ориентации (или референции) при принятии решений:
Внутренняя. Вы ориентируетесь на собственное мнение, принципы, убеждения и идеалы.
Внешняя. Вы ориентируетесь на чужое мнение, поддаетесь чужому влиянию.
Старайтесь сформировать у себя внутреннюю референцию – особенно по вопросам взаимоотношений.
Вас всегда будут окружать самые разнообразные люди со своим жизненным опытом и психологическими особенностями. Их мнение – не абсолют, особенно если они рассказывают вам о других людях. Они сами могли в прошлом поддаться на эффект Розенталя и составить негативное или излишне позитивное мнение о человеке, и теперь передают его вам.
Поэтому не делайте поспешных выводов о ком-либо, проверяйте все сами при личном общении. Начинайте каждое новое знакомство «с чистого листа» – так, будто вы никогда ничего не слышали об этом человеке. Доверяйте себе.
3. Используйте сигналы обратной связи
Помните – даже мельчайшие сигналы в общении (мимика, жесты, позы, интонации) корректируют поведение и мышление вашего собеседника, заставляют его «отзеркаливать» ваше отношение. Поэтому, если хотите произвести хорошее впечатление и добиться успеха в беседе, всегда будьте лояльны к собеседнику. Больше дружелюбия, открытости, проявлений доверия, приятных замечаний.
Особенно хорошо эта рекомендация действует в командной работе. Если хотите добиться хорошего и быстрого результата в каком-либо деле – проявите свое доверие к партнерам, возлагайте на них большие надежды и не стесняйтесь говорить об этом. Но, конечно же, по итогам работы не спешите винить их за свои нереализованные ожидания – люди могут ошибаться, и это нормально. Также старайтесь сами работать на свой максимум и показывать (а не рассказывать!) положительный пример коллегам.
А вы сталкивались с эффектом Розенталя в жизни? Он вам скорее вредил, или помогал? Поделитесь своим опытом!
И будьте здоровы!
Соль премии[править]
Фишка Перельмана в следующем. Вернемся назад на стопицот лет, когда все люди были сильно уверены, что Земля плоская. А все потому, что не мог тогдашний анонимус посмотреть на Землю сильно издалека и убедиться, что земля на самом деле нифига не плоская, а вовсе даже шарообразная.
Мораль в том, что если смотреть сильно вблизи, поверхность шарика (сфера) неотличима от плоскости.
Двинемся дальше. Возьмем обычный круг на плоскости. У него есть граница — окружность.
Ёжу понятно, что если вырезать этот круг ножницами, а потом стянуть границу в одну точку и надуть, что получится, воздухом, то круг расправится в двумерную сферу (тут надо думать о воздушных шарах и все такое).
Мораль — двумерная сфера получается из круга склеиванием всех точек границы в одну. И наоборот, если вырезать в двумерной сфере маленькую дырку и растянуть её, то двумерная сфера расправится в плоский круг.
Аналогично, если взять обычный шарик и склеить все точки его границы в одну, то получится трёхмерная сфера. Анонимус, не пытайся сделать это в домашних условиях — не выскочив в четырёхмерное пространство, это нереально.
Аналогично, наше трёхмерное пространство — это просто трёхмерная сфера с вырезанной дыркой. Если смотреть на трёхмерную сферу вблизи, то её нельзя отличить от трёхмерного пространства — типа дырка сильно далеко, и мы её не замечаем.
Так вот. Трёхмерная сфера — пример трёхмерного многообразия (это значит, что, глядя вблизи, она неотличима от трёхмерного пространства).
На самом деле, разных трёхмерных многообразий столько же, сколько натуральных чисел. Взглянуть на них издалека мы не можем — воображения не хватает. А вблизи они все устроены одинаково. Как быть?
Давным давно расовый французский математик Пуанкаре высказал гипотезу, что если трёхмерное многообразие удовлетворяет некоторым свойствам, то ничем иным, кроме трёхмерной сферы, оно быть не может. Потом пиндосский институт Клея решил, что если кто это докажет — то тот сильно вумный и заслуживает миллиона денег.
Лет тридцать назад расовый пиндос Терстон придумал, что хоть трёхмерных многообразий и сильно много, но они все должны быть устроены вроде конструктора LEGO. То есть, достаточно задаться восемью типами деталек и по-разному клеить их друг к другу, чтобы можно было получить вообще все возможные трёхмерные многообразия. Идея была шибко красивая, но опять же, доказать её Терстон не мог. Позже она получила название «гипотеза геометризации». Среди деталек Терстона только одна удовлетворяла условиям Пуанкаре — трёхмерная сфера. То есть, доказательство гипотезы геометризации влекло бы за собой доказательство гипотезы Пуанкаре.
Сама по себе гипотеза Пуанкаре мало кому нахер сдалась, примерно как и теорема Ферма. Гипотеза геометризации гораздо важнее.
Доказательство этой гипотезы и есть заслуга Гриши. За это ему сразу, как только поняли, что доказательство правильное, дали Филдса и 15k, от коих он отказался. И немедленно стали говорить о том, что ему дадут миллион. Но по правилам института Клея, для того, чтобы претендовать на миллион, нужно, чтобы доказательство было опубликовано в уважаемом журнале (Nature, например). Гриша же сразу положил с прибором на формальности и опубликовался в интернетах. Поэтому так долго и тянули кота за хвост.
Сurriculum vitæ. Первые страницы
Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде в семье инженера-электрика и учительницы математики, а спустя десять лет у него появилась сестра – в будущем тоже кандидат (точнее, PhD) математических наук. Помимо любви к классической музыке, привитой матерью, Григорий с детства проявлял интерес к точным наукам: в пятом классе он начал посещать математический центр при Дворце пионеров, а после восьмого перешел в школу № 239 с углубленным изучением математики, которую окончил без золотой медали только из-за недостатка баллов по нормативам ГТО. В 1982 году он в составе школьной команды получил золотую медаль на 23-й Международной математической олимпиаде в Будапеште и вскоре был зачислен на математико-механический факультет Ленинградского государственного университета без сдачи экзаменов.
В вузе за примерную учебу Перельман получал Ленинскую стипендию. Окончив университет с отличием, он поступил в аспирантуру на базе Ленинградского отделения Математического института имени В. А. Стеклова РАН. В 1990 году под научным руководством академика Александра Даниловича Александрова (основоположника так называемой геометрии Александрова – раздела метрической геометрии) Перельман защитил кандидатскую диссертацию на тему «Седловые поверхности в евклидовых пространствах». Затем в должности старшего научного сотрудника продолжил работать в лаборатории математической физики института Стеклова, успешно развивая теорию пространств Александрова.
В начале 1990-х Перельману довелось поработать в нескольких уважаемых исследовательских учреждениях США: в Университете штата Нью-Йорк в Стоуни-Брук, Курантовском институте математических наук и Калифорнийском университете в Беркли.

Поворотной для молодого математика стала встреча с Ричардом Гамильтоном, область научных интересов которого простиралась в плоскости дифференциальной геометрии – нового направления, широко используемого в общей теории относительности. В своих работах по топологии многообразий американский ученый впервые использовал систему дифференциальных уравнений под названием поток Риччи – нелинейный аналог уравнения теплопроводности, который описывает не распределение температуры, а деформацию хаусдорфова пространства, локально эквивалентного евклидовому.
Благосклонность зарубежного коллеги и столь фундаментальная проблема произвели на Перельмана большое впечатление. В то время он продолжал сглаживать углы пространств Александрова – технические трудности казались непреодолимыми, и ученый вновь и вновь возвращался к идее потока Риччи. По словам советского математика Михаила Громова, сосредоточившись на этих задачах, Перельман стал еще более аскетичным, что вызывало тревогу у его близких.
В 1994 году он получил приглашение прочесть лекцию на Международном конгрессе математиков в Цюрихе, а сразу несколько научных организаций, в том числе Принстонский и Тель-Авивский университеты, предложили ему место в штате. В ответ на просьбу Стэнфордского университета предоставить резюме и рекомендации ученый заметил: «Если они знают мои работы, им не нужно мое CV. Если же они нуждаются в моем CV, они не знают мои работы». Несмотря на такое обилие заманчивых предложений, в 1995 году он принял решение вернуться в «родной» институт Стеклова.
Помимо непритязательности в быту, пристрастия к музыке (Перельман играет на скрипке) и строгой приверженности научной этике, ученого уже тогда отличал интерес к параллельному решению сложных задач. В 1994 году он доказал гипотезу о душе. В дифференциальной геометрии под «душой» (S) подразумевают компактное тотально выпуклое тотально геодезическое подмногообразие риманова многообразия (M, g). В простейшем случае, то есть в случае евклидова пространства Rn (n отражает мерность), душой будет любая точка этого пространства.
Перельман доказал, что душа полного связного риманова многообразия с секционной кривизной K ≥ 0, секционная кривизна одной из точек в котором строго положительна во всех направлениях, является точкой, а само многообразие диффеоморфно Rn. Математиков потрясло редкостное изящество доказательства Перельмана: выкладки заняли всего две страницы, в то время как «доперельмановские» попытки решения излагались в длинных статьях и оставались незавершенными.
Убийство Кеннеди и эффект Манделы
Одна из самых известных, не только в англоязычном сегменте интернета «мандел», связана с изменением обстоятельств убийства президента США Джона Кеннеди. Очень многие помнят, что в автомобиле президента в момент убийства находилось четыре человека, а не шесть как сейчас во всех видео и фото документах. Более того, многие помнят, что автомобиль был белого цвета. Но, оказывается это еще не все изменения, которые произошли в тот злополучный день 22 ноября 1963 года. Оказывается, что чета Коннелли (губернатора) не встречали президента на летном поле, как это сейчас преподносится а прилетели с ним одним самолетом.
Удивительно «во-время» появляются «новые» данные, обеспечивающие логичность происходящего, так чтобы комар носа не подточил. Когда говорят «автомобиль президента», очевидно, что это именно автомобиль из президентского гаража, проверенный, с усиленным двигателем, со всякими дополнительными причиндалами. Существует видеоролик трансляции прибытия президента в Даллас. Там показано что прилетело несколько самолетов, один из них явно транспортный. Логично предположить, что именно в нем и прилетел автомобиль президента. Так вот, что бросилось в глаза. Белый автомобиль на фото в Форт-Уэрте это похоже именно тот, четырехместный, на котором ехал в Далласе Кеннеди в другой реальности. Тот факт, что губернатор с супругой теперь оказывается были с президентом в Форт-Уэрте, а не встречали его в аэропорту Далласа, «логично» объясняет почему появился шестиместный автомобиль — губернатора с супругой надо было разместить…»

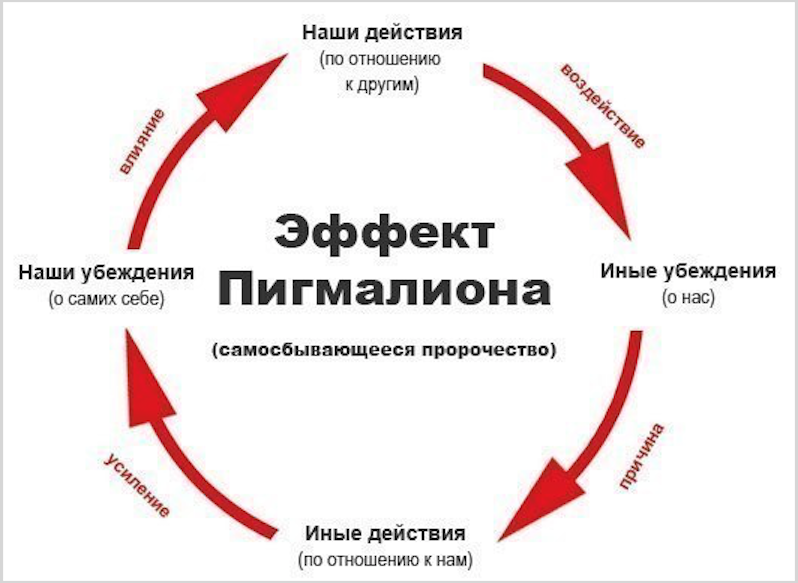
Как использовать Эффект Пигмалиона в своих целях?
Эффект Пигмалиона буквально способен изменить жизнь человека. И дело не в магии. Те сигналы, которые подает нам наше окружение, в совокупности влияют на нашу жизнь, решают добьемся успеха или нет. Чья-то мимолетная похвала, взгляд, интонация формируют у нас ощущение того, что мы это можем. Вера других подпитывает нас и направляет в правильное русло.
Тоже касается и наших ожиданий в свой собственный адрес. Люди, уверенные в себе и своих способностях, формируют характер и поведение таким образом, что все их действия приводят к желанному результату. Наблюдая негативное влияние феномена (которое также называют эффектом Голума), можно его контролировать и не поддаваться плохим установкам.
Ведь плохие ожидания равнозначны порочному кругу. Человек думает, что все будет плохо, срабатывает феномен Розенталя, все становится действительно плохо и, таким образом, подтверждает мысли человека. Нужно больше усилие, чтобы начать верить в хорошее на фоне плохих обстоятельств.
Но если мы будем искренне будем верить, что наши дети, родители или вторые половинки способны на большее, то подтолкнем их к значительным успехам. Отчасти в этом и проявляется распространенная в последнее время техника визуализации желаний. Необходимо говорить своим детям, что они все смогут, у них все получится, и так оно будет на самом деле.
Зная, как работает эффект Розенталя, можно добиться больших успехов, взяв его под контроль. Для руководителей он полезен повышением производительности компании. Нужно только научиться позитивно думать о своих работниках, верить в них и периодически показывать им это. Результат не заставит себя ждать.
Но стоит помнить о том, что у каждого человека есть предел возможностей. Не стоит ставить слишком высоких планок, они уничтожают мотивацию. Цель должна быть сложной, но достижимой. Только тогда показатели роста эффективности пойдут вверх.
Социальная психология. Эффект Пигмалиона в экспериментах Розенталя.
Сам по себе эффект не является методом совершенствования интеллекта или духовных качеств, но он отличный мотиватор.
Затворничество
На сегодняшний день ни словом, ни делом не напоминает о себе Григорий Перельман. Где живет этот выдающийся человек? В Ленинграде, в одной из обычных многоэтажек в Купчино. Вместе с матерью живет Григорий Перельман. Личная жизнь у него не сложилась. Однако математик не оставляет надежды завести семью.

Григорий Яковлевич с российскими журналистами не общается. Свои контакты он сохранил только с зарубежной прессой. Однако, несмотря на затворничество, интерес к этому человеку не угасает. О нем пишут книги. Григория Перельмана нередко упоминают в научных статьях и очерках. Где сейчас Григорий Перельман? По-прежнему на родине. Многие считают, что услышат это имя еще не раз, а может быть, и в связи с решением очередной «проблемы тысячелетия».
Прайминг и интеллект
Пример со студентами, который мы привели выше, демонстрирует, как безобидный разговор на внешне отвлеченную тему о футбольных
фанатах решил исход экзамена, повлияв на способность студентов концентрироваться и решать узкоспециализированные логические
задачи.
Множество подобных экспериментов разной степени жесткости, проведенных Канеманом позволили подтвердить: напоминание о прошлом
мгновенно переключает мозг на мысли, которые с ним связаны.
Соответственно, «плохое» прошлое вызывает негативные ассоциации и мыслеобразы, воспоминания о хорошем – позитивные.
В результате способность адекватно мыслить и решать задачи в настоящем меняется в позитивную или негативную сторону.
Прайминг и агрессия
Зная о степени влияния на наше бессознательное, манипулятор может легко получить доступ к нашей эмоциональной сфере.
Это подтверждается экспериментально. Попробуйте сами: предложите группе собравшихся игру в два этапа.
В первой части предложите вытащить из колоды карточки со словами различного эмоционального содержания.
Карточки из колоды раскладываются на игровом поле без определенной логики.
По умолчанию на половине карточек должны быть написаны слова с негативной эмоциональной привязкой: убийца, вор, казнокрад,
распутник, война, кровопролитие, насилие, etc.
Вторая половина карточек заполняется словами, несущими нейтральный эмоциональный заряд: погода, перемещение, космос, вода,
сноровка, рождение… .
Вторую часть игры можно посвятить опросу мнения о ком-то из известных политиков.
Вам бросится в глаза, насколько резкими, категоричными и агрессивными окажутся мнения тех, кому в первой части игры достались
«негативные» карточки.
И насколько более взвешенными и рассудительными в сравнении оказались мнения людей, доставших карточки «нейтральные».
Обратите внимание, что скорее всего смысл самих слов, записанных на карточке не имел никакого отношение ни к политике, ни к
тому политическому персонажу, который предлагалось оценить.
Эффект Пашена – Бака
В сильном магнитном поле связь между орбитальными и спиновыми моментами терпит разрыв, и они становятся независимыми друг к другу в отношении магнитного поля. В таком случае дополнительную энергию, которая связывается с магнитными моментами можно определить как:
Разрешенные переходы должны отвечать правилам отбора:
Как следствие, возникновение простого триплета Зеемана.
Если в сильном магнитном поле расщепление линий оказывается больше, чем тонкое расщепление, такой эффект называется эффектом Пашена – Бака.
Увеличивая напряженность внешнего магнитного поля, в начале (около $H\approx 0$), можно наблюдать тонкое расщепление линий спектра, далее аномальный эффект Зеемана (мультиплет) и в сильном магнитном поле получить нормальный эффект Зеемана — триплет.
Самой сложной является картина расщепления линий спектра при промежуточных величинах магнитного поля.
Пример 1
Задание: Определите вид эффекта Зеемана (нормальный или аномальный) для линий спектра, который наблюдают в слабом магнитном поле для перехода ${}^3{D_1}\to {}^3{P_0}$.
Решение:
Рассмотрим начальный терм: ${}^3{D_1}$. Для него имеем: $L=2,$ мультиплетность $\tau =3,$ следовательно, $S=\frac{\tau -1}{2}=1$, $J=1.$ Вычислим фактор Ланде ($g_1$):
\
Магнитное квантовое число будет принимать три значения:
\
Исследуем конечный терм ${}^3{P_0}$. Для него имеем: L=1, $\tau =3\to S=1\ .$ При $J=0$ расщепления нет. Смещение по частоте для расщепленных линий вычислим в соответствии с формулой:
\
Правило отбора для квантовых чисел:
\
Линия спектра может расщепиться не более, чем на 3 составляющие, получили нормальный эффект Зеемана.
Ответ: Простой эффект Зеемана.
Пример 2
Задание: Какое число подуровней получится при расщеплении в слабом магнитном поле терма ${}^2{F_{\frac{5}{2}}}$?
Решение:
Расщепление линий связывают с расщеплением самих энергоуровней, так как атом, имеющий магнитный момент, во внешнем магнитном поле получает дополнительную энергию:
\
где ${\mu }_{{\rm b}}$ – магнетон Бора$;$ $g$ – фактор Ланде$;$ ${{\rm m}}_{{\rm J}}{\rm =}{\rm J},{\rm J}{\rm -}{\rm 1,\dots ,-}{\rm J}.\ $Если фактор Ланде не равен нулю, то терм в слабом магнитном поле может расщепиться на $2J+1$ подуровень. Если $g=0$, то расщепления не происходит. Рассмотрим предложенный терм (${}^2{F_{\frac{5}{2}}}$) и вычислим фактор Ланде. Мы имеем: $L=3,\ J=\frac{5}{2},\ S=\frac{2-1}{2}=\frac{1}{2},$ соответственно:
\
Так как $g\ne 0$, то расщепление происходит и число подуровней равно:
\
Ответ: 6 подуровней.
Затворник и бессеребренник
Неискушенному в точных науках человеку крайне сложно будет понять, что именно доказал Григорий. Только профессионалы-математики и большие любители этой науки, обладающие фундаментальными знаниями, могут в полной мере оценить значение сделанного им открытия и его неординарность. Достаточно сказать, что это открытие Перельмана светила мировой науки назвали «открытием тысячелетия».
В 2006 году учёному присудили за это открытие международную премию «Медаль Филдса» – «За вклад в геометрию и его революционные идеи в изучение геометрической и аналитической структуры потока Риччи». Поразив общественность, гений отказался её принимать. Он мотивировал это тем, что он не согласен с тем, как сегодня организовано математическое общество. Во многом Перельман полагает его устройство несправедливым.Кроме того, интересно, что суть теории Пуанкаре попросту можно изложить так: если трёхмерная поверхность в чём-то похожа на сферу, то её можно расправить в сферу. Из-за этой краткой формулировки гипотезу Пуанкаре называют ещё «Формулой Вселенной»
В этом кроется вся её важность и суть отказа Перельмана от всех премий. Он просто сказал: «Я знаю, как управлять Вселенной
Скажите, в таком случае, зачем мне бежать за миллионом?»
Поначалу Перельман не отказывался общаться с прессой. Он охотно давал интервью. Потом он понял, что журналистов по большей части занимает не наука и его открытие, а его внешний вид и личная жизнь. Соседи первое время удивлялись шумихе вокруг скромной особы Перельмана, потом привыкли. Когда у них спрашивали почему Григорий так себя ведёт, те говорили, что он всегда был очень скромным и закрытым, привык довольствоваться малым. Он не считает важными богатство и славу, его увлекает только наука.Долгое время в прессе муссировались слухи, что математик живёт на пенсию матери. Это, конечно же, неправда. Он долгое время читал лекции в США, зарабатывал прилично. Кроме того проценты от публикаций научных трудов тоже весьма солидные. Работа у математика тоже есть. Он трудится над какими-то секретными разработками в сфере нанотехнологий по приглашению одной шведской компании. В Стокгольме живёт его сестра, а он туда только иногда приезжает. Работодатели не связывают гения какими-либо неудобными для него обязательствами.
Денег у Григория Перельмана хватает. Просто в нашем сегодняшнем мире, где все стремятся побольше урвать, а стилем жизни стало хвастовство о своей красивой жизни в соцсетях, обывателю весьма сложно понять, что не все люди такие. Есть те, кому все эти излишества ни к чему. Иногда учёного видят в поношенной старой одежде и тогда начинают появляться разные грязные статьи в прессе.
Подписывайтесь на нас в Telegram
Культурология
t.me
О Перельмане чего только не выдумывали за это время! Некоторое время, а может и сейчас тоже, математиком интересовались как отечественные, так и зарубежные спецслужбы. Это неудивительно, учитывая масштаб открытия гениального учёного. Ведь ему удалось постичь некие сверхзнания, которые могут помочь понять основы мироздания.
Тем временем Григорий всё также живёт со своей пожилой мамой на окраине Санкт-Петербурга. Он не женат, у него нет детей. Это неудивительно. Он женат на науке. Григорий непритязателен в быту и еде. Его не волнует мода. Ну и что? У гениев свои причуды. Автомобиля у Перельмана нет. Он привык передвигаться пешком и говорит, что ходьба активизирует работу мозга. Он старается проходить до 40 километров в день. Возможно, новые, ещё более захватывающие открытия ещё впереди!Гениальные учёные всегда кажутся обычным людям, мягко говоря, странными. Лёгкая сумасшедшинка – это обязатеьны спутник уникума. Прочтите в другой нашей статье об ещё одном великом учёном – история и сокровенные тайны безумного учёного-гения: отец современной астрономии Тихо Браге.
Напишите в комментариях, что Вы думаете по этому поводу?
- Как шедеврально подделаные письма Клеопатры, Иуды и других исторических личностей совершили революцию в науке
- В чём секрет гениального изобретения Никола Теслы, способного остановить все войны на Земле
- Какие тайны отношений между Джеки Кеннеди и Елизаветой II раскрыл недавно агент секретной службы